题目内容
4.在等比数列{an}中,a2+a4=20,a3+a5=40,则数列{an}的前n项和Sn=2n+1-2.分析 利用等比数列的通项公式与求和公式即可得出.
解答 解:设等比数列{an}的公比为q,∵a2+a4=20,a3+a5=40,
则q(a2+a4)=20q=40,解得q=2,∴${a}_{1}(2+{2}^{3})$=20,解得a1=2.
则数列{an}的前n项和Sn=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2.
故答案为:2n+1-2.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
14.已知a>1,$x={log_a}\sqrt{2}+\frac{1}{2}{log_a}3$,$y=\frac{1}{2}{log_a}5$,$z={log_a}\sqrt{21}-{log_a}\sqrt{3}$,则( )
| A. | x>y>z | B. | z>y>x | C. | y>x>z | D. | z>x>y |
15.用二分法找函数f(x)=2x+3x-7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )
| A. | (0,1) | B. | (0,2) | C. | (2,3) | D. | (2,4) |
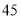 名,女同学
名,女同学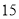 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个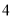 人的课外兴趣小组.
人的课外兴趣小组.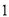 名同学做实验,该同学做完后,再从小组内剩下的同学中选
名同学做实验,该同学做完后,再从小组内剩下的同学中选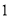 名同学做实验,求选出的两名同学中恰有
名同学做实验,求选出的两名同学中恰有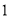 名女同学的概率;
名女同学的概率; ,第二次做实验的同学得到的实验数据为
,第二次做实验的同学得到的实验数据为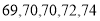 ,请问哪位同学的实验更稳定?并说明理由.
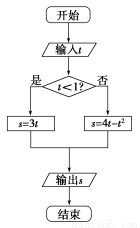
,请问哪位同学的实验更稳定?并说明理由.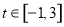 ,则输出的s属于( )
,则输出的s属于( )