题目内容
8.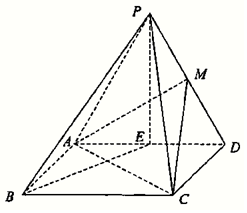 如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD中点,PE⊥BE,PA=PD=AD=2,AB=$\sqrt{2}$.(Ⅰ)求证:PB∥平面MAC;
(Ⅱ)求证:PE⊥平面ABCD;
(Ⅲ)求证:平面MAC⊥平面PBE.
分析 (Ⅰ)连接BD,交AC于O,连接OE,则OM∥PB,利用线面平行的判定定理证明:PB∥平面MAC;
(Ⅱ)证明PE⊥AD,利用PE⊥BE,BE∩AD=E,证明:PE⊥平面ABCD;
(Ⅲ)证明AC⊥平面PBE,即可证明:平面MAC⊥平面PBE.
解答 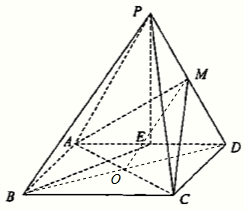 (Ⅰ)连接BD,交AC于O,连接OE,则OM∥PB,
(Ⅰ)连接BD,交AC于O,连接OE,则OM∥PB,
∵PB?平面MAC,OM?平面MAC,
∴PB∥平面MAC;
(Ⅱ)∵PA=PD,E是AD的中点,
∴PE⊥AD,
∵PE⊥BE,BE∩AD=E,
∴PE⊥平面ABCD;
(Ⅲ)∵PE⊥平面ABCD,AC?平面ABCD,
∴AC⊥PE,
∵AD=2,AB=$\sqrt{2}$,四边形ABCD是矩形,E是AD中点,
∴△ABE∽△DAC,
∴∠ABE=∠DAC,
∴AC⊥BE,
∵PE∩BE=E,
∴AC⊥平面PBE,
∵AC?平面MAC,
∴平面MAC⊥平面PBE.
点评 本题考查线面平行、线面垂直的证明,考查面面垂直的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
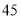 名,女同学
名,女同学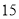 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个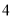 人的课外兴趣小组.
人的课外兴趣小组.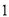 名同学做实验,该同学做完后,再从小组内剩下的同学中选
名同学做实验,该同学做完后,再从小组内剩下的同学中选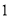 名同学做实验,求选出的两名同学中恰有
名同学做实验,求选出的两名同学中恰有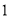 名女同学的概率;
名女同学的概率; ,第二次做实验的同学得到的实验数据为
,第二次做实验的同学得到的实验数据为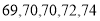 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由. 的解集为
的解集为 ,则
,则
 。
。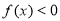 ,且f(1)=﹣2
,且f(1)=﹣2