题目内容
已知A、B、C是 的三内角,向量
的三内角,向量 ,
, ,且
,且 .
.
(1)求角A;
(2)若 ,求
,求 .
.
(1) ;(2)
;(2)
解析试题分析:(1)用向量数量积公式列出方程 ,在用化一公式将其化为
,在用化一公式将其化为 ,根据三角形内角的范围为
,根据三角形内角的范围为 ,求出整个角
,求出整个角 的范围,最后确定
的范围,最后确定 的值,即得到A的值。(2)将1用
的值,即得到A的值。(2)将1用 表示,
表示, 用2倍角公式展开,得到
用2倍角公式展开,得到 ,因为
,因为 ,所以将上式两边都同时除以
,所以将上式两边都同时除以 即得到关于
即得到关于 的一元二次方程,可求得
的一元二次方程,可求得 的值。将角C写成
的值。将角C写成 ,用诱导公式及正切的两角和公式即可求得
,用诱导公式及正切的两角和公式即可求得 .
.
试题解析:(1)∵ ∴
∴ ,即
,即 …3分
…3分 ,
, 
∵ ,
, ,∴
,∴ ,
,
即 . 6
. 6
(2)由题知: ,即:
,即: ,
,
∵ ,∴
,∴ ,∴
,∴ 或
或 ; 10分
; 10分
而 使
使 ,故
,故 应舍去,∴
应舍去,∴ ,
,
∴
= . 12分
. 12分
考点:向量数量级,二倍角公式,同角函数基本关系式,正切的两角和公式

练习册系列答案
相关题目
 和钝角
和钝角 的终边分别与单位圆交于
的终边分别与单位圆交于 两点.
两点. ,求
,求 的值;
的值; 是单位圆上的一点,且
是单位圆上的一点,且 ,求
,求 和
和 的夹角
的夹角 .
.
 为锐角,
为锐角, ,
, ,求
,求 的值.
的值.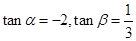 ,其中
,其中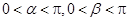 .
.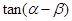 的值;
的值;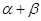 的值.
的值. ,
, 是第三象限角,
是第三象限角, .
. 的值;
的值; 的值.
的值. .
. 三个内角A,B,C所对的边,向量
三个内角A,B,C所对的边,向量 ,设
,设
 ,求角
,求角 ;
; ,求三角形ABC的面积.
,求三角形ABC的面积. 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,已知
,已知 .
. 的值;
的值; ,求
,求 sin20°cos80°的值.
sin20°cos80°的值.