题目内容
如下图,在平面直角坐标系中,锐角 和钝角
和钝角 的终边分别与单位圆交于
的终边分别与单位圆交于 两点.
两点.
(1)若 两点的纵坐标分别为
两点的纵坐标分别为 ,求
,求 的值;
的值;
(2)已知点 是单位圆上的一点,且
是单位圆上的一点,且 ,求
,求 和
和 的夹角
的夹角 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由 两点的纵坐标,可得
两点的纵坐标,可得 ,
, 正余弦值,进而求得
正余弦值,进而求得 ;(2)利用向量的数量积可求得
;(2)利用向量的数量积可求得 和
和 的夹角余弦,得出
的夹角余弦,得出 .
.
解:(1)因为 两点的纵坐标分别为
两点的纵坐标分别为 ,
,
所以 ,
, ,
,
又因为 为锐角,
为锐角, 为钝角,
为钝角,
所以 ,
, ,
,
所以 . 4分
. 4分
(2)因为 是单位圆上的一点,所以
是单位圆上的一点,所以 ,
, ,
,
又因为 ,所以
,所以 ,
,
因为点 是单位圆上的一点,所以
是单位圆上的一点,所以 ,即
,即 ,
,
整理得, ,
,
所以 ,
,
又因为 ,
,
所以 和
和 的夹角为
的夹角为 . 9分
. 9分
考点:三角恒等变换,向量的数量积的坐标运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 sin(2x+
sin(2x+ )+6sinxcosx-2cos2x+1,x∈R.
)+6sinxcosx-2cos2x+1,x∈R. ]上的最大值和最小值.
]上的最大值和最小值. ,
,
 ;
; 。
。 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若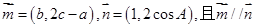 .
. ,求函数
,求函数 上的取值范围.
上的取值范围. 都是锐角,且
都是锐角,且 ,
, ,求
,求 的值.
的值. ,
, , 且
, 且 ,
, , 求
, 求 的值.
的值. ,cos(α+β)=-
,cos(α+β)=- ,0<α<
,0<α< ,π<α+β<
,π<α+β< π,求cosβ的值.
π,求cosβ的值. 的三内角,向量
的三内角,向量 ,
, ,且
,且 .
. ,求
,求 .
.