题目内容
已知: 三个内角A,B,C所对的边,向量
三个内角A,B,C所对的边,向量 ,设
,设
(1)若 ,求角
,求角 ;
;
(2)在(1)的条件下,若 ,求三角形ABC的面积.
,求三角形ABC的面积.
(1) ;(2)三角形ABC的面积为
;(2)三角形ABC的面积为 .
.
解析试题分析:(1)由向量数量积坐标计算公式可得函数 的表达式,利用三角函数的有关公式(倍角公式、辅助角公式等)将其化简得
的表达式,利用三角函数的有关公式(倍角公式、辅助角公式等)将其化简得 ,由已知
,由已知 ,列出方程
,列出方程 ,即可求得角
,即可求得角 的值;(2)由已知条件
的值;(2)由已知条件 ,化为
,化为 ,结合正弦定理可得:
,结合正弦定理可得: ,由此得
,由此得 ,进而求出角
,进而求出角 的值.有三角形内角和定理得
的值.有三角形内角和定理得 ,联立
,联立 ,可求出角
,可求出角 和
和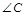 ,最后可求得三角形ABC的面积.
,最后可求得三角形ABC的面积.
试题解析:(1)
因为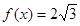 ,即
,即 ,所以
,所以 或
或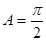 (舍去) 6分
(舍去) 6分
(2)由 ,则
,则 ,
,
所以 ,又因为
,又因为 ,所以
,所以
所以三角形ABC是等边三角形,由 ,所以面积为
,所以面积为 . 12分
. 12分
考点:1.向量数量积运算;2.利用三角恒等变换求角;3.正弦定理、余弦定理解三角形,求三角形的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,cos(α+β)=-
,cos(α+β)=- ,0<α<
,0<α< ,π<α+β<
,π<α+β< π,求cosβ的值.
π,求cosβ的值. 的三内角,向量
的三内角,向量 ,
, ,且
,且 .
. ,求
,求 .
. 中,角
中,角 所对的边为
所对的边为 ,角
,角 为锐角,若
为锐角,若 ,
, 且
且 .
. 的大小;
的大小; ,求
,求 .
. .
. 的最大值及取得最大值时x的值;
的最大值及取得最大值时x的值; ,
,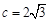 ,
, ,求△ABC的面积.
,求△ABC的面积. 的内角A、B、C所对的边为
的内角A、B、C所对的边为 ,
,  ,
,  ,且
,且 与
与 所成角为
所成角为 .
. 的取值范围.
的取值范围.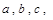 且对
且对 是常数,
是常数, .
. 的值;
的值; 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在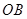 上,设矩形
上,设矩形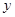 .
.
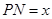 ,将
,将 的函数关系式;
的函数关系式;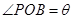 ,将
,将 的函数关系式.
的函数关系式. <α<
<α< ,0<β<
,0<β< ,
, +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值.