题目内容
11.在△ABC中,角A,B,C的对边分别是a,b,c,已知b=2,c=2$\sqrt{2}$,且C=$\frac{π}{4}$,则△ABC的面积为$\sqrt{3}+1$.分析 由已知利用正弦定理可求sinB,结合B的范围,利用特殊角的三角函数值可求B,利用三角形内角和定理可求A,进而利用三角形面积公式即可计算得解.
解答 解:由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}⇒sinB=\frac{bsinC}{c}=\frac{1}{2}$,
又c>b,且B∈(0,π),
所以$B=\frac{π}{6}$,
所以$A=\frac{7π}{12}$,
所以$S=\frac{1}{2}bcsinA=\frac{1}{2}×2×2\sqrt{2}sin\frac{7π}{12}=\frac{1}{2}×2×2\sqrt{2}×\frac{{\sqrt{6}+\sqrt{2}}}{4}=\sqrt{3}+1$.
故答案为:$\sqrt{3}+1$.
点评 本题主要考查了正弦定理,特殊角的三角函数值,三角形内角和定理,三角形面积公式在解三角形中的综合应用,考查了转化思想,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
6.执行如图所示的程序框图,则输出的结果为( )
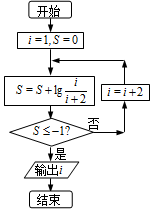

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
16.已知三个数1,a,9成等比数列,则圆锥曲线$\frac{x^2}{a}+\frac{y^2}{2}=1$的离心率为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{5}$或$\frac{{\sqrt{10}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$或$\frac{{\sqrt{10}}}{2}$ |
1.双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$右焦点到渐近线的距离为( )
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{12}{5}$ |
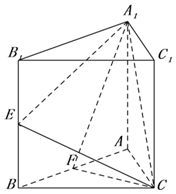 正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.
正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.