Question

已知函数f（x）=lnx-

1

2

ax²+bx．
（1）当b=a-1时，讨论f（x）的单调性；
（2）当a=0时，若函数f（x）有两个不同的零点，求b的取值范围；
（3）在（2）的条件下，设x₁、x₂为函数f（x）的两个不同的零点．求证：x₁x₂＞e²（e为自然对数的底）．

Answer 1

考点：利用导数研究函数的单调性,利用导数研究函数的极值

专题：导数的综合应用

分析：（1）当b=a-1时，求函数的导数，利用函数单调性和导数之间的关系，即可判断f（x）的单调性；
（2）当a=0时，若函数f（x）有两个不同的零点，利用数形结合即可求b的取值范围；
（3）求函数的导数，构造函数，根据x₁、x₂为函数f（x）的两个不同的零点，即可证明不等式．

解答： 解：解：（1）函数f（x）的定义域为（0，+∞），
f′（x）=

1

x

-ax+a-1=

-ax2+(a-1)+1

x

=-

(ax+1)(x-1)

x

…（2分）
当a≥0时，因为ax+1＞0，故函数f（x）在（0，1）上递增，在（1，+∞）上递减…（3分）
当-1＜a＜0时，函数f（x）在（0，1）和（-

1

a

，+∞）上递增，在（1，-

1

a

）上递减…（4分）
当a=-1时，f′（x）＞0，函数f（x）在（0，+∞）递增，
当a＜-1时，函数f（x）在（0，-

1

a

）和（1，+∞）上递增，在（-

1

a

，1）上递减…（6分）
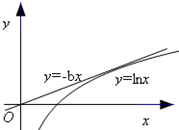
（2）当a=0，f（x）=lnx+bx，令g（x）=lnx，h（x）=-bx，
要使得f（x）有两个零点，即使得g（x）和h（x）图象有两个交点（如图）…（6分）
容易求得g（x）和h（x）的切点为（e，1），所以0＜-b＜

1

e

，即-＜

1

e

＜b＜0．（8分）
（3）∵x₁、x₂为函数f（x）的两个零点，不妨设0＜x₁＜x₂，
所以lnx₁+bx₁=0，lnx₂+bx₂=0，
两式相减得：

lnx2-lnx1

x2-x1

=-b，两式相加得：

lnx2+lnx1

x2+x1

=-b …（9分）
要证x₁x₂＞e²，即证lnx₁+lnx₂＞2，
即证

lnx2-lnx1

x2-x1

＞

2

x2+x1

，即证ln

x2

x1

＞

2( x2 x1 -1)

x2 x1 +1

 …（11分）
令t=

x2

x1

，（t＞1），即证lnt＞

2(t-1)

t+1

，
h（t）=lnt-

2(t-1)

t+1

，则h′（t）=

(t-1)2

t(t+1)

＞0…（12分）
所以h（t）＞h（1）=0，即lnt＞

2(t-1)

t+1

，（t＞1）（13分）
所以

lnx2-lnx1

x2-x1

＞

2

x2+x1

，所以x₁x₂＞e²…（14分）

点评：本题主要考查函数单调性和导数之间的关系，考查考生的应用，运算量大，综合性较强，属于难题．