题目内容
6. 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.(Ⅰ)在平面A1B1C1D1内,请作出过点E与CE垂直的直线l,并证明l⊥CE;
(Ⅱ)设(Ⅰ)中所作直线l与CE确定的平面为α,求直线CC1和平面α所成角的大小.
分析 (Ⅰ)连接B1E,C1E,则直线B1E即为所求直线l,推导出B1E⊥CC1,B1E⊥C1E,由此能证明l⊥CE.
(Ⅱ)连接B1C,则平面CEB1即为平面α,推导出B1E⊥C1F,C1F⊥平面α,从而直线CC1和平面α所成角为∠FCC1,由此能求出直线CC1和平面α所成角.
解答 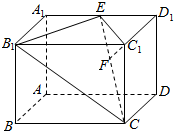 解:(Ⅰ)如图所示,连接B1E,C1E,则直线B1E即为所求直线l…(3分)
解:(Ⅰ)如图所示,连接B1E,C1E,则直线B1E即为所求直线l…(3分)
∵在长方体ABCD-A1B1C1D1中,CC1⊥平面A1B1C1D1
∴B1E⊥CC1…(4分)
∵B1C1=2A1B1=4,E是A1D1的中点
∴B1E⊥C1E…(5分)
又CC1∩C1E=C1
∴B1E⊥平面CC1E
∴B1E⊥CE,即l⊥CE…(6分)
(Ⅱ)如图所示,连接B1C,则平面CEB1即为平面α
过点C1作C1F⊥CE于F…(7分)
由(Ⅰ)知B1E⊥平面CC1E,故B1E⊥C1F
∵C1F⊥CE,CE∩B1E=E
∴C1F⊥平面CEB1,即C1F⊥平面α…(9分)
∴直线CC1和平面α所成角为∠FCC1…(10分)
∵在△ECC1中,$E{C_1}=C{C_1}=2\sqrt{2}$,且EC1⊥CC1
∴$∠FC{C_1}={45^0}$…(11分)
∴直线CC1和平面α所成角为45°.…(12分)
点评 本题考查过点垂直于已知直线的直线的作法与证明,考查线面角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
7.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\\{y≤a(x-4)}\end{array}\right.$,若z=x+2y的最大值为2,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
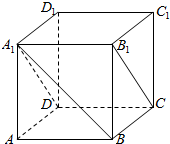 (1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.
(1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明. 某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:
某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:
 在某校科普知识竞赛前的模拟测试中,得到甲、乙两名学生的6次模拟测试成绩(百分制)的茎叶图;
在某校科普知识竞赛前的模拟测试中,得到甲、乙两名学生的6次模拟测试成绩(百分制)的茎叶图;