题目内容
如图1,在矩形ABCD中,AD=2,AB=4,E,F分别为边AB,AD的中点.现将△ADE沿DE折起,得四棱锥A-BCDE(如图2).
(1)求证:EF∥平面ABC;
(2)若平面ADE⊥平面BCDE,求四面体FDCE的体积.

(1)求证:EF∥平面ABC;
(2)若平面ADE⊥平面BCDE,求四面体FDCE的体积.

考点:平面与平面垂直的判定,直线与平面平行的判定
专题:计算题,证明题,空间位置关系与距离
分析:(1)取线段AC的中点M,连结MF、MB,可证明EF∥BM,从而证明EF∥平面ABC;(2)CE为三棱锥C-EFD的高.进而求四面体FDCE的体积.
解答:
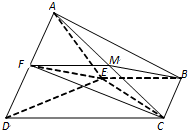 解:(1)证明:取线段AC的中点M,连结MF、MB.
解:(1)证明:取线段AC的中点M,连结MF、MB.
∵F为AD的中点,
∴MF∥CD,且MF=
CD.
在折叠前,四边形ABCD为矩形,E为AB的中点,
∴BE∥CD,且BE=
CD.
∴MF∥BE,且MF=BE.
∴四边形BEFM为平行四边形,
∴EF∥BM.又EF?平面ABC,BM?平面ABC,
∴EF∥平面ABC.
(2)在折叠前,四边形ABCD为矩形,AD=2,AB=4,E为AB的中点,
∴△ADE、△CBE都是等腰直角三角形,且AD=AE=EB=BC=2.
∴∠DEA=∠CEB=45°,且DE=EC=2
.
又∵∠DEA+∠DEC+∠CEB=180°,
∴∠DEC=90°.
又∵平面ADE⊥平面BCDE,
平面ADE∩平面BCDE=DE,CE?平面BCDE,
∴CE⊥平面ADE,即CE为三棱锥C-EFD的高.
∵F为AD的中点,
∴S△EFD=
×
×AD•AE=
×2×2=1.
∴四面体FDCE的体积V=
×S△EFD•CE=
×1×2
=
.
 解:(1)证明:取线段AC的中点M,连结MF、MB.
解:(1)证明:取线段AC的中点M,连结MF、MB.∵F为AD的中点,
∴MF∥CD,且MF=
| 1 |
| 2 |
在折叠前,四边形ABCD为矩形,E为AB的中点,
∴BE∥CD,且BE=
| 1 |
| 2 |
∴MF∥BE,且MF=BE.
∴四边形BEFM为平行四边形,
∴EF∥BM.又EF?平面ABC,BM?平面ABC,
∴EF∥平面ABC.
(2)在折叠前,四边形ABCD为矩形,AD=2,AB=4,E为AB的中点,
∴△ADE、△CBE都是等腰直角三角形,且AD=AE=EB=BC=2.
∴∠DEA=∠CEB=45°,且DE=EC=2
| 2 |
又∵∠DEA+∠DEC+∠CEB=180°,
∴∠DEC=90°.
又∵平面ADE⊥平面BCDE,
平面ADE∩平面BCDE=DE,CE?平面BCDE,
∴CE⊥平面ADE,即CE为三棱锥C-EFD的高.
∵F为AD的中点,
∴S△EFD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴四面体FDCE的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
点评:本题需要分析作出辅助线,构造平行,注意一条在平面内,另一条在平面外,用线面平行判定定理证明线面平行,求体积要选择底面,同时兼顾高,以达到简化运算的目的.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
 如图四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,又二面角P-CD-B为45°
如图四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,又二面角P-CD-B为45° 如图,边长为1的正方形ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则
如图,边长为1的正方形ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则