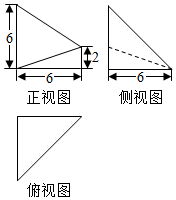
题目内容
11.定义在R上的偶函数y=f(x),当x≥0时,f(x)=2x-4,则不等式f(x)≤0的解集是[-2,2].分析 根据条件判断函数的单调性和函数的零点,利用函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:当x≥0时,由f(x)=2x-4=0得x=2,
且当x≥0时,函数f(x)为增函数,
∵f(x)是偶函数,
∴不等式f(x)≤0等价为f(|x|)≤f(2),
即|x|≤2,即-2≤x≤2,
即不等式的解集为[-2,2],
故答案为:[-2,2].
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.

练习册系列答案
相关题目
6.设集合A={x|x≥-1},B={x|y=$\sqrt{3x-1}$},则A∩∁RB等于( )
| A. | {x|-1≤x$<\frac{1}{3}$} | B. | {x|-$\frac{1}{3}<x<2$} | C. | {x|-1$≤x≤\frac{1}{3}$} | D. | {x|-$\frac{1}{3}≤x≤2$} |
16.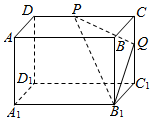 在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,P、Q分别是棱CD、CC1上的动点,如图.当BQ+QD1的长度取得最小值时,二面角B1-PQ-D1的余弦值的取值范围为( )
在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,P、Q分别是棱CD、CC1上的动点,如图.当BQ+QD1的长度取得最小值时,二面角B1-PQ-D1的余弦值的取值范围为( )
 在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,P、Q分别是棱CD、CC1上的动点,如图.当BQ+QD1的长度取得最小值时,二面角B1-PQ-D1的余弦值的取值范围为( )
在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,P、Q分别是棱CD、CC1上的动点,如图.当BQ+QD1的长度取得最小值时,二面角B1-PQ-D1的余弦值的取值范围为( )| A. | [0,$\frac{1}{5}$] | B. | [0,$\frac{\sqrt{10}}{10}$] | C. | [$\frac{1}{5}$,$\frac{\sqrt{10}}{10}$] | D. | [$\frac{\sqrt{10}}{10}$,1] |
20.已知数列{an}的前n项和Sn=p×2n+2,{an}是等比数列的充要条件是( )
| A. | p=1 | B. | p=2 | C. | p=-1 | D. | p=-2 |
1.数列{an}是公差不为0的等差数列,且a1,a3,a7为正项等比数列{bn}的第5,7,9项,则数列{bn}的公比为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |