题目内容
2.已知函数f (x)=ln x+$\frac{1}{x}$-1,g(x)=$\frac{x-1}{lnx}$(Ⅰ)求函数 f (x)的最小值;
(Ⅱ)求函数g(x)的单调区间;
(Ⅲ)求证:直线 y=x不是曲线 y=g(x)的切线.
分析 (Ⅰ)求出f(x)的导数,求得单调区间,可得极小值,且为最小值;
(Ⅱ)求出g(x)的定义域,求出导数,结合函数f(x)的单调区间,即可得到g(x)的单调区间;
(Ⅲ)运用反证法证明,假设直线y=x是曲线g(x)的切线.设切点为(x0,y0),运用导数的几何意义,以及点满足曲线的方程,推理得到矛盾,即可得证.
解答 解:(Ⅰ)函数f(x)的定义域为(0,+∞),
$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
所以f(x)的最小值为0;
(Ⅱ)函数g(x)的定义域为(0,1)∪(1,+∞),
$g'(x)=\frac{{lnx-(x-1)\frac{1}{x}}}{{{{ln}^2}x}}=\frac{{lnx+\frac{1}{x}-1}}{{{{ln}^2}x}}=\frac{f(x)}{{{{ln}^2}x}}$,
由(Ⅰ)得,f(x)≥0,所以g'(x)≥0,
所以g(x)的单调增区间是(0,1),(1,+∞),无单调减区间;
(Ⅲ)证明:假设直线y=x是曲线g(x)的切线.
设切点为(x0,y0),则g'(x0)=1,即$\frac{{ln{x_0}+\frac{1}{x_0}-1}}{{{{ln}^2}{x_0}}}=1$,
又${y_0}=\frac{{{x_0}-1}}{{ln{x_0}}},{y_0}={x_0}$,则$\frac{{{x_0}-1}}{{ln{x_0}}}={x_0}$.
所以$ln{x_0}=\frac{{{x_0}-1}}{x_0}=1-\frac{1}{x_0}$,得g'(x0)=0,与 g'(x0)=1矛盾,
所以假设不成立,直线y=x不是曲线g(x)的切线
点评 本题考查导数的运用:求单调区间、极值和最值,考查反证法的运用,注意推理得出矛盾,考查化简整理的运算能力,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且3$\overrightarrow{a}$+2$\overrightarrow{b}$与λ$\overrightarrow{a}$-$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | 1 |
17.已知复数z1=1+ai,z2=3+2i,a∈R,i为虚数单位,若z1z2为实数,则a=( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
14.已知正三棱锥S-ABC,底面是边长为1的正三角形,侧棱长为2,若过直线AB的截面,将正三棱锥的体积分成两个相等的部分,则截面与底面所成二面角的平面角的余弦值为( )
| A. | $\frac{\sqrt{15}}{10}$ | B. | $\frac{4\sqrt{15}}{15}$ | C. | $\frac{\sqrt{15}}{15}$ | D. | $\frac{2\sqrt{15}}{15}$ |
12.已知命题p:?x∈R,x+$\frac{4}{x}$≥4;命题q:?x0∈(0,∞),log2x0=$\frac{1}{2}$,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
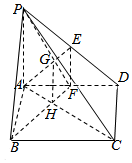 如图,在底面为正方形的四棱锥P-ABCD中,PA⊥底面ABCD,AP=AD,取线段PD,AD的中点E,F,连结AE,PF交于一点G.连结BF交AC于点H.
如图,在底面为正方形的四棱锥P-ABCD中,PA⊥底面ABCD,AP=AD,取线段PD,AD的中点E,F,连结AE,PF交于一点G.连结BF交AC于点H.