题目内容
现有命题:①若x∈C,则|x|≥x;②若|z|=z,则z必为实数;③若a=b,则z=(a2-b2)+(a+b)i(a,b∈R)为纯虚数;④若x∈C,则|x|≥
其中假命题有 .
| |x|2 |
考点:复数的基本概念
专题:数系的扩充和复数
分析:①若x=2i,则|x|=2,与x无法比较大小,即可判断出正误;
②设z=a+bi(a,b∈R),可得
=a+bi,利用复数相等可得b=0,z必为实数,即可判断出正误;
③若取a=b=0,则z=(a2-b2)+(a+b)i=0为实数,即可判断出正误;
④若x∈C,设x=a+bi(a,b∈R),利用复数模的计算公式即可判断出正误.
②设z=a+bi(a,b∈R),可得
| a2+b2 |
③若取a=b=0,则z=(a2-b2)+(a+b)i=0为实数,即可判断出正误;
④若x∈C,设x=a+bi(a,b∈R),利用复数模的计算公式即可判断出正误.
解答:
解:①若x=2i,则|x|=2,与x无法比较大小,不正确;
②设z=a+bi(a,b∈R),∵|z|=z,∴
=a+bi,因此b=0,则z必为实数,正确;
③若a=b=0,则z=(a2-b2)+(a+b)i=0为实数,不正确;
④若x∈C,设x=a+bi(a,b∈R),则|x|=
,
=
=
,正确.
其中假命题有①④.
故答案为:①④.
②设z=a+bi(a,b∈R),∵|z|=z,∴
| a2+b2 |
③若a=b=0,则z=(a2-b2)+(a+b)i=0为实数,不正确;
④若x∈C,设x=a+bi(a,b∈R),则|x|=
| a2+b2 |
| |x|2 |
(
|
| a2+b2 |
其中假命题有①④.
故答案为:①④.
点评:本题考查了复数模的计算公式、复数相等、复数为实数及纯虚数的充要条件,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=x3+ax2+bx+c,且0≤f(1)=f(2)=f(3)<10,那么( )
| A、0≤c<10 | B、-6≤c<4 |
| C、c>4 | D、c≤-6 |
已知a=5 log23.4.b=5 log23.6,c=(
) log20.3,则有( )
| 1 |
| 5 |
| A、a>b>c |
| B、b>a>c |
| C、a>c>b |
| D、c>a>b |
已知命题p:?x∈R,x-2>lgx,命题q:?x∈R,ex>1,则( )
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∧(¬q)是真命题 |
| D、命题p∨(¬q)是假命题 |
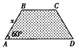 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9