题目内容
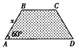 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9| 3 |
| 3 |
考点:根据实际问题选择函数类型
专题:函数的性质及应用
分析:设出高h,利用条件列出h与x的关系,通过面积公式表示出BC,然后列出不等式组,求出腰长x的取值范围.
解答:
解:设高为h,又9
=
(AD+BC),其中AD=BC+2•
=BC+x,h=
x,
∴9
=
(2BC+x)
x,得BC=
-
,由
得2≤x<6.
故答案为:[2,6).
| 3 |
| 1 |
| 2 |
| x |
| 2 |
| ||
| 2 |
∴9
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 18 |
| x |
| x |
| 2 |
|
故答案为:[2,6).
点评:本题考查实际问题的应用,面积公式以及不等式组的解法,考查分析问题解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示的方格纸中有定点O,P,Q,E,F,G,H,则
+
=( )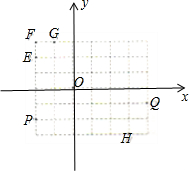
| OP |
| OQ |

A、
| ||
B、
| ||
C、
| ||
D、
|
已知不等式组
表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k的取值范围是( )
|
A、(0,
| ||
B、[-
| ||
C、(-∞,
| ||
D、(-∞,-
|