题目内容
若关于x，y的不等式组
表示的区域为三角形，则实数a的取值范围是（ ）
|
| A、（-∞，1） |
| B、（0，1） |
| C、（-1，1） |
| D、（1，+∞） |
考点：简单线性规划
专题：不等式的解法及应用
分析：根据题意，画出不等式组表示的平面区域，再结合图象，利用数形结合的方法得到a的范围
解答：
解：画出不等式组对应的可行域如图：
要使可行域为三角形，需要直线y=ax的斜率a在-1与1之间，即-1＜a＜1，
则a的取值范围是（-1，1）．
故选：C．
要使可行域为三角形，需要直线y=ax的斜率a在-1与1之间，即-1＜a＜1，
则a的取值范围是（-1，1）．
故选：C．
点评：本题考查画不等式组表示的平面区域、考查数形结合的数学思想方法．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
“a=2”是“l1：ax+4y-1=0与l2：x+ay+3=0平行”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f（x）=
的值域是（ ）
| 1-x2012 |
| 1+x2012 |
| A、[-1，1] |
| B、（-1，1] |
| C、[-1，1） |
| D、（-1，1） |
已知函数f（x）是R上的奇函数，且在R上有f′（x）＞0，则f（1）的值 （ ）
| A、恒为正数 | B、恒为负数 |
| C、恒为0 | D、可正可负 |
已知命题“若p，则q”是真命题，对下列命题中一定是真命题的是（ ）
| A、若q，则p |
| B、￢p，则￢q |
| C、若￢q，则￢p |
| D、若￢p，则q |
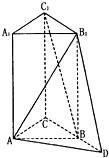已知正三棱柱ABC-A1B1C1中，AA1=2AC=4，延长CB至D，使CB=BD．
直三棱柱ABC-A1B1C1中，AB⊥AC，AC=AA1，AC1与A1C交于一点P，延长B1B到D，使得BD=
如图，已知正方形ABCD的边长为6，点E，F分别在边AB，AD上，AE=AF=4，现将△AEF沿线段EF折起到△A′EF位置，使得A′C=2