题目内容
14.椭圆的中心在原点,焦点在x轴上,焦距与短半轴相等,且经过点(0,2),则该椭圆的方程是$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.分析 由题意可知,椭圆是焦点在x轴上的椭圆,方程可设为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,且b=c=2,结合隐含条件求得a,则椭圆方程可求.
解答 解:由题意可知,椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$.
且b=c=2.
∴a2=b2+c2=4+4=8.
则椭圆方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
故答案为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
点评 本题考查椭圆方程的求法,考查了椭圆的简单性质,是基础题.

练习册系列答案
相关题目
5.已知关于x的不等式ax2+2x+b>0(a≠0)的解集是{x|x≠-$\frac{1}{a}$,x∈R},且a>b,则$\frac{{a}^{2}+{b}^{2}}{a-b}$的最小值是( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
2.设集合S={y|y=2x,x∈R},T={(x,y)|y=x2+1,x∈R},则S∩T是( )
| A. | ∅ | B. | {0} | C. | {(0,1)}和{(1,2)} | D. | {1} |
18.函数y=2sin(-x+$\frac{π}{6}$)在下列哪个区间上增函数( )
| A. | [$\frac{5π}{6}$,$\frac{11π}{6}$] | B. | [$\frac{2π}{3}$,$\frac{5π}{3}$] | C. | [$\frac{π}{2}$,$\frac{3π}{2}$] | D. | [-$\frac{π}{2}$,0] |
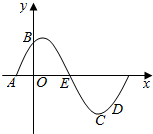 已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.
已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)一个周期内的图象上的四个点,如图所示,A(-$\frac{π}{6}$,0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,$\overrightarrow{CD}$在x轴方向上的投影为$\frac{π}{12}$.