题目内容
5.已知关于x的不等式ax2+2x+b>0(a≠0)的解集是{x|x≠-$\frac{1}{a}$,x∈R},且a>b,则$\frac{{a}^{2}+{b}^{2}}{a-b}$的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
分析 由已知得ab=1,从而$\frac{{a}^{2}+{b}^{2}}{a-b}$=$\frac{(a-b)^{2}+2}{a-b}$=(a-b)+$\frac{2}{a-b}$,由此利用基本不等式能求出$\frac{{a}^{2}+{b}^{2}}{a-b}$的最小值.
解答 解:∵关于x的不等式ax2+2x+b>0(a≠0)的解集是{x|x≠-$\frac{1}{a}$,x∈R},且a>b,
∴a>0,且对应方程有两个相等的实根为-$\frac{1}{a}$
由根与系数的故关系可得-$\frac{1}{a}$•(-$\frac{1}{a}$)=$\frac{b}{a}$,即ab=1
故$\frac{{a}^{2}+{b}^{2}}{a-b}$=$\frac{(a-b)^{2}+2}{a-b}$=(a-b)+$\frac{2}{a-b}$,
∵a>b,∴a-b>0,
由基本不等式可得(a-b)+$\frac{2}{a-b}$≥2$\sqrt{(a-b)•\frac{2}{a-b}}$≥2$\sqrt{2}$,
当且仅当a-b=$\sqrt{2}$时取等号.
故$\frac{{a}^{2}+{b}^{2}}{a-b}$的最小值为:2$\sqrt{2}$.
故选:A.
点评 本题考查代数式的最小值的求法,是基础题,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
10.“a=2”是“函数f(x)=xa-2为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.极限$\underset{lim}{x→+∞}$[cos$\sqrt{x+1}$-cos$\sqrt{x}$]的结果是( )
| A. | 无穷大 | B. | 0 | ||
| C. | -$\frac{1}{2}$ | D. | 不存在,也不是无穷大 |
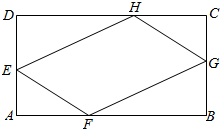 如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.
如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.