题目内容
9.若关于x的不等式x2+|x+a|<2至少有一个正数解,则实数a的取值范围是(-$\frac{9}{4}$,2).分析 先将不等式写成:|x+a|<2-x2,再构造两函数f(x)=|x+a|,g(x)=2-x2,最后运用函数的图象和性质解不等式.
解答 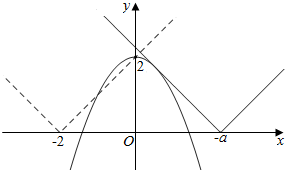 解:不等式可写成:|x+a|<2-x2,(*)
解:不等式可写成:|x+a|<2-x2,(*)
根据题意,不等式(*)至少有一个正数解,
即至少存在一个正数x0使得:|x0+a|<2-x02,
记f(x)=|x+a|,g(x)=2-x2,画出两函数的图象,
①当f(x)的顶点(-a,0)(a<0)在x轴右侧时,
两函数图象在右侧相切是临界,如图(蓝线):
此时,-(x+a)=2-x2,即x2-x-a-2=0,
由△=0,解得a=-$\frac{9}{4}$,
所以,要使不等式(*)至少有一个正数解,则a>-$\frac{9}{4}$,
②当f(x)图象的顶点(-a,0)(a>0)在x轴左侧时,
函数g(x)的图象过点(0,2)也是临界,如图(红线),
此时,a=2,要使原不等式有正数解,则a<2,
综合以上讨论得,实数a的取值范围为:(-$\frac{9}{4}$,2),
故答案为:(-$\frac{9}{4}$,2).
点评 本题主要考查了含绝对值不等式的解法,以及函数图象与性质的综合应用,体现了分类讨论和数形解的解题思想,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
17.极限$\underset{lim}{x→+∞}$[cos$\sqrt{x+1}$-cos$\sqrt{x}$]的结果是( )
| A. | 无穷大 | B. | 0 | ||
| C. | -$\frac{1}{2}$ | D. | 不存在,也不是无穷大 |
20.A、B、C、D四人站成一排照相,A和B必须站在一起的站法有( )种.
| A. | 6 | B. | 12 | C. | 24 | D. | 8 |
17.已知复数z满足(3+4i)z=25,则$\overline{z}$=( )
| A. | 3-4i | B. | 3+4i | C. | -3-4i | D. | -3+4i |
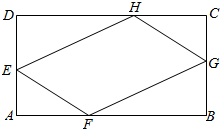 如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.
如图,在矩形ABCD中,已知AD=1.5,AB=a(a>1.5),E,F,G,H分别是边AD,AB,BC,CD上的动点,且满足AE=AF=CG=CH.若AE=x,当x变化时.