题目内容
19.已知函数f(x)=alnx+$\frac{{x}^{2}}{2}$-(a+1)x,a∈R..(Ⅰ)若函数f(x)在区间(1,3)上单调递减,求a的取值范围;
(Ⅱ)当a=-1时,证明f(x)≥$\frac{1}{2}$.
分析 (Ⅰ)求出函数的导数,根据函数的单调性求出a的范围即可;
(Ⅱ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值即可.
解答 解:(I)函数的定义域为(0,+∞).
因为$f'(x)=\frac{a}{x}+x-(a+1)=\frac{{{x^2}-(a+1)x+a}}{x}=\frac{(x-1)(x-a)}{x}$.
又因为函数f(x)在(1,3)单调减,所以不等式(x-1)(x-a)≤0在(1,3)上成立.
设g(x)=(x-1)(x-a),则g(3)≤0,即9-3(a+1)+a≤0即可,解得a≥3.
所以a的取值范围是[3,+∞).…(7分)
(Ⅱ)当a=-1时,f(x)=-lnx+$\frac{{x}^{2}}{2}$,
f′(x)=$\frac{(x+1)(x-1)}{x}$,
令f'(x)=0,得x=1或x=-1(舍).
当x变化时,f(x),f'(x)变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
所以$f(x)≥\frac{1}{2}$成立.…(13分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
相关题目
7.已知向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为120°,若向量$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}$,且$\overrightarrow{a}⊥\overrightarrow{c}$,则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |
14.若f(x)=$\frac{1}{2}$ax2+2x-lnx(a≠0)在区间[1,2]上是增函数,则实数a的最小值为( )
| A. | 1 | B. | -1 | C. | -$\frac{3}{4}$ | D. | -2 |
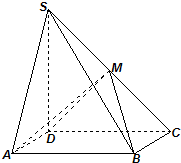 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.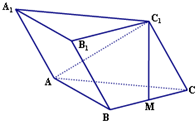 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.