题目内容
在平面内,设到定点F(0,2)和x轴距离之和为4的点P轨迹为曲线C,直线l过点F,交曲线C于M,N两点.
(1)说明曲线C的形状,并画出图形;
(2)求线段MN长度的范围.
(1)说明曲线C的形状,并画出图形;
(2)求线段MN长度的范围.
考点:轨迹方程,两点间的距离公式
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设动点P(x,y),利用到定点F(0,2)和x轴距离之和为4,建立方程,分类讨论,化简可得方程,从而说明曲线C的形状,并画出图形;
(2)分类讨论,利用当l过BD时,|MN|最小,最小值为4,当l过C(或A)时,|MN|最大,即可求线段MN长度的范围.
(2)分类讨论,利用当l过BD时,|MN|最小,最小值为4,当l过C(或A)时,|MN|最大,即可求线段MN长度的范围.
解答:
 解:(1)设动点P(x,y),由已知得:
解:(1)设动点P(x,y),由已知得:
+|y|=4 (1分)
当y≥0时,化简得:x2=-4(y-3)
当y<0时,化简得:x2=12(y+1)(3分)
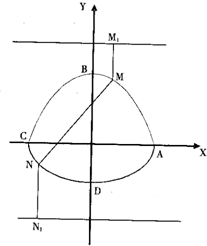
∴如图:曲线C是焦点在F(0,2),准线分别为y=-4和y=4,顶点分别是(0,-1)和(0,3)的两条抛物线一部分组成的封闭图形ABCD…(6分)
(2)当M、N在两支抛物线上时,过M、N分别作相应准线的垂线,垂足分别是M1、N1,由抛物线定义,MM1=MF;NN1=NF,
设M、N的纵坐标分别为y1,y2,|MN|=8-(|y1|+|y2|)
当l过BD时,|MN|最小,最小值为4,
当l过C(或A)时,|MN|最大,
此时直线l的方程为-x+
y=2
和抛物线x2=-4(y-3)
另一个交点M(
,
),|MN|最大值为
,
∴|MN|范围是[4,
](10分)
同理,当M、N都在上支抛物线上时,|MN|范围也是[4,
]
∴由上综述:|MN|范围是[4,
](13分)
 解:(1)设动点P(x,y),由已知得:
解:(1)设动点P(x,y),由已知得:| x2+(y-2)2 |
当y≥0时,化简得:x2=-4(y-3)
当y<0时,化简得:x2=12(y+1)(3分)
∴如图:曲线C是焦点在F(0,2),准线分别为y=-4和y=4,顶点分别是(0,-1)和(0,3)的两条抛物线一部分组成的封闭图形ABCD…(6分)
(2)当M、N在两支抛物线上时,过M、N分别作相应准线的垂线,垂足分别是M1、N1,由抛物线定义,MM1=MF;NN1=NF,
设M、N的纵坐标分别为y1,y2,|MN|=8-(|y1|+|y2|)
当l过BD时,|MN|最小,最小值为4,
当l过C(或A)时,|MN|最大,
此时直线l的方程为-x+
| 3 |
| 3 |
另一个交点M(
| 2 | ||
|
| 8 |
| 3 |
| 16 |
| 3 |
∴|MN|范围是[4,
| 16 |
| 3 |
同理,当M、N都在上支抛物线上时,|MN|范围也是[4,
| 16 |
| 3 |
∴由上综述:|MN|范围是[4,
| 16 |
| 3 |
点评:本题考查轨迹与轨迹方程,考查分类讨论的数学思想,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某几何体的三视图如图所示,则该几何体的表面积( )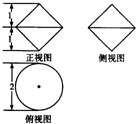

A、
| ||
B、2
| ||
C、(2
| ||
D、(2
|
若等比数列{an}的前3项的和S3=14,且a2=4,公比大于1,则a7=( )
| A、182 | B、46 |
| C、64 | D、128 |
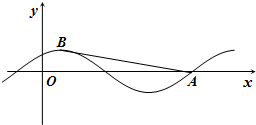 已知函数f(x)=2
已知函数f(x)=2