题目内容
4.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个顶点A(0,1),离心率为$\frac{\sqrt{2}}{2}$,过左焦点F1的直线l交椭圆于C,D两点,右焦点为F2.(Ⅰ)求椭圆的标准方程;
(Ⅱ)若|CF2|,|CD|,|DF2|成等差数列,求直线l的方程.
分析 (Ⅰ)利用已知条件求出b,通过离心率,以及椭圆的几何量的关系,求出a,即可得到椭圆的标准方程.
(Ⅱ)利用|CF2|,|CD|,|DF2|成等差数列,得到|CF2|+|DF2|=2|CD|,求出|CD|.当斜率存在时,设直线l的方程为y=k(x+1),联立方程组,设C(x1,y1),D(x2,y2),利用韦达定理以及弦长公式,求出k,得到直线l的方程.验证当斜率不存在时,经检验不成立.
解答 解:(Ⅰ)因为A(0,1)为椭圆的一个顶点,所以b=1,
又离心率为$\frac{{\sqrt{2}}}{2}$,即$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,
解方程组$\left\{\begin{array}{l}b=1\\ \frac{c}{a}=\frac{{\sqrt{2}}}{2}\\{a^2}={b^2}+{c^2}\end{array}\right.$
得$a=\sqrt{2},b=1,c=1$,
所以椭圆方程为$\frac{x^2}{2}+{y^2}=1$.(4分)
(Ⅱ)因为|CF2|,|CD|,|DF2|成等差数列,所以|CF2|+|DF2|=2|CD|①,(5分)
又因为$|{C{F_2}}|+|{D{F_2}}|+|{CD}|=4a=4\sqrt{2}$ ②,由 ①②解得,$|{CD}|=\frac{{4\sqrt{2}}}{3}$.(7分)
当斜率存在时,设直线l的方程为y=k(x+1),联立方程组$\left\{\begin{array}{l}y=k(x+1)\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,
得x的方程(2k2+1)x2+4k2x+2k2-2=0,
因为直线过椭圆的左焦点,显然△>0,
设C(x1,y1),D(x2,y2),
由韦达定理${x_1}+{x_2}=-\frac{{4{k^2}}}{{2{k^2}+1}}$,${x_1}{x_2}=\frac{{2{k^2}-2}}{{2{k^2}+1}}$,
代入弦长公式,$|{CD}|=\sqrt{(1+{k^2})[{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}]}$=$\sqrt{(1+{k^2})[{{{({-\frac{{4{k^2}}}{{2{k^2}+1}}})}^2}-4×\frac{{2{k^2}-2}}{{2{k^2}+1}}}]}$=$\frac{{4\sqrt{2}}}{3}$
整理得7k4-2k2-5=0,解得${k^2}=1,{k^2}=-\frac{5}{7}$(舍),k=±1,
所以直线l的方程为y=x+1或y=-x-1.
当斜率不存在时,经检验不成立.(12分)
点评 本题考查直线与椭圆的位置关系的综合应用,椭圆标准方程的求法,考查转化思想以及计算能力.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | 2 | B. | 3$\sqrt{2}$ | C. | 1 | D. | 4 |
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |

| A. | 13 | B. | 12 | C. | 22 | D. | 11 |
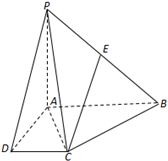 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.