题目内容
9.已知f(x)=$\left\{\begin{array}{l}x+2\\{x^2}\\-2x+8\end{array}$$\begin{array}{l}({x≤-1})\\({-1<x<2})\\({x≥2})\end{array}$(1)画出f(x)的图象;
(2)求f(f(-1))的值;
(3)方程f(x)=a有两个不同的实根,求实数a的范围.
分析 (1)由分段函数的画法,可得f(x)的图象;
(2)先求f(-1)=1,再求f(f(-1))=f(1),由分段函数式计算即可得到所求;
(3)由题意转化为函数y=f(x)的图象和直线y=a有两个交点,通过图象观察,即可得到所求a的范围.
解答 解:(1)由分段函数
f(x)=$\left\{\begin{array}{l}x+2\\{x^2}\\-2x+8\end{array}$$\begin{array}{l}({x≤-1})\\({-1<x<2})\\({x≥2})\end{array}$,
可得图象如右: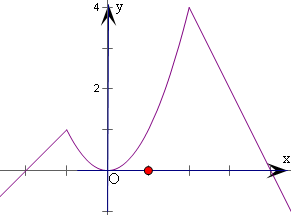
(2)f(-1)=-1+2=1,
f(f(-1))=f(1)=1;
(3)方程f(x)=a有两个不同的实根,
即为函数y=f(x)的图象和直线y=a有两个交点.
由图象可得,a的范围是(-∞,0)∪(1,4).
点评 本题考查分段函数的图象和应用:求函数值和方程的根的个数,考查数形结合的思想方法和转化思想的运用,考查运算能力,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
14.下列函数既是奇函数,又在(0,+∞)上单调递增的是( )
| A. | y=-x2 | B. | y=x3 | C. | y=log2x | D. | y=-3-x |
18.过两直线x-2y+2=0和2x+y-1=0的交点且斜率为1的直线方程为( )
| A. | x-y-1=0 | B. | x+y-1=0 | C. | x-y+1=0 | D. | x+y+1=0 |
19.已知圆C的圆心是直线$\left\{\begin{array}{l}{x=t}\\{y=1+t}\end{array}\right.$(t为参数)与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为( )
| A. | (x+1)2+y2=2 | B. | (x-1)2+y2=2 | C. | x2+(y+1)2=2 | D. | x2+(y-1)2=2 |
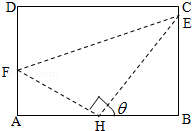 如图,矩形ABCD的内接Rt△FHE,(H是直角顶点),H是AB的中点,E,F分别落在线段BC,AD上.已知AB=2,AD=$\sqrt{3}$,记∠BHE=θ.
如图,矩形ABCD的内接Rt△FHE,(H是直角顶点),H是AB的中点,E,F分别落在线段BC,AD上.已知AB=2,AD=$\sqrt{3}$,记∠BHE=θ.