题目内容
直线l:y=ax+1与双曲线C:3x2-y2=1相交于A,B两点,O为坐标原点.
(1)a为何值时,以AB为直径的圆过原点?
(2)是否存在实数a,使|
|=|
|且
+
=λ(2,1)?若存在,求a的值;若不存在,说明理由.
(1)a为何值时,以AB为直径的圆过原点?
(2)是否存在实数a,使|
| OA |
| OB |
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)将y=ax+1代入方程3x2-y2=1,得(a2-3)x2+2ax+2=0,设交点为A(x1,y1),B(x2,y2),由以AB为直径的圆经过圆点,得x1x2=-y1y2,由此能求出a=±1.
(2)假设存在实数a满足条件,则(x1+x2,y1+y2)=λ(2,1),x12+y12=x22+y22,由此能求出存在a=-2满足条件.
(2)假设存在实数a满足条件,则(x1+x2,y1+y2)=λ(2,1),x12+y12=x22+y22,由此能求出存在a=-2满足条件.
解答:
解:(1)将y=ax+1代入方程3x2-y2=1,
得3x2-(ax+1)2=1,
整理,得(a2-3)x2+2ax+2=0,
设交点为A(x1,y1),B(x2,y2),
则x1+x2=-
,x1x2=
,
所以,y1y2=(ax1+1)(ax2+1)=a2•x1x2+a(x1+x2)+1=1
因为以AB为直径的圆经过圆点
所以OA⊥OB,故OA与OB的斜率的乘积为-1.
∴x1x2=-y1y2,
即
=-1,解得a=±1.
(2)假设存在实数a满足条件.
∵
+
=λ(2,1),∴(x1+x2,y1+y2)=λ(2,1),
又|
|=|
|,∴x12+y12=x22+y22,
即(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
∴2λ(x1-x2)+λ(y1-y2)=0,
∴a=
=-
=-2.
故存在a=-2满足条件.
得3x2-(ax+1)2=1,
整理,得(a2-3)x2+2ax+2=0,
设交点为A(x1,y1),B(x2,y2),
则x1+x2=-
| 2a |
| a2-3 |
| 2 |
| a2-3 |
所以,y1y2=(ax1+1)(ax2+1)=a2•x1x2+a(x1+x2)+1=1
因为以AB为直径的圆经过圆点
所以OA⊥OB,故OA与OB的斜率的乘积为-1.
∴x1x2=-y1y2,
即
| 2 |
| a2-3 |
(2)假设存在实数a满足条件.
∵
| OA |
| OB |
又|
| OA |
| OB |
即(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,
∴2λ(x1-x2)+λ(y1-y2)=0,
∴a=
| y1-y2 |
| x1-x2 |
| 2λ |
| λ |
故存在a=-2满足条件.
点评:本题考查以AB为直径的圆过原点时实数a的值的求法,考查是否存在实数a,使|
|=|
|且
+
=λ(2,1)的判断与求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.
| OA |
| OB |
| OA |
| OB |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=
的值域是( )
| 3x-1 |
| 3x+1 |
| A、(-1,1) |
| B、[-1,1] |
| C、(-1,1] |
| D、[-1,1) |
sin(600°)的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
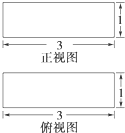
在具有如图所示的正视图和俯视图的几何体中,体积最小的几何体的表面积为 ( )

| A、13 | ||
B、7+3
| ||
C、
| ||
| D、14 |
函数f(x)=1-
在其定义域上是( )
| 2 |
| 2x+1 |
| A、单调递增的奇函数 |
| B、单调递增的减函数 |
| C、偶函数且在(0,+∞)上单调递增 |
| D、偶函数且在(0,+∞)上单调递减 |
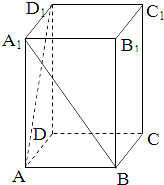 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|