题目内容
已知中心在原点,焦点在x轴上的椭圆的焦距等于4
,它的一条弦所在直线方程是x-y+4=0,若此弦的中点坐标为(-3,1),求椭圆的方程.
| 6 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设出焦点在x轴上的椭圆的标准方程,再设出直线与椭圆的两个交点的坐标,代入椭圆方程,利用点差法得到
=-
,代入中点坐标和直线的斜率,得到a,b的关系,结合椭圆的焦距及隐含条件求解a2,b2的值,则椭圆方程可求.
| (x1-x2)(x1+x2) |
| a2 |
| (y1-y2)(y1+y2) |
| b2 |
解答:
解:由题意设椭圆方程为
+
=1(a>b>0),
再设直线x-y+4=0与椭圆的两个交点为A(x1,y1),B(x2,y2),
则
+
=1,
+
=1,
作差得:
=-
,
即
=-
,
∵弦的中点坐标为(-3,1),∴-
=1,即a2=3b2 ①,
∵2c=4
,c=2
②,
又a2=b2+c2 ③,
联立①②③得:a2=36,b2=12.
∴椭圆的方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
再设直线x-y+4=0与椭圆的两个交点为A(x1,y1),B(x2,y2),
则
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
作差得:
| (x1-x2)(x1+x2) |
| a2 |
| (y1-y2)(y1+y2) |
| b2 |
即
| y1-y2 |
| x1-x2 |
| b2(x1+x2) |
| a2(y1+y2) |
∵弦的中点坐标为(-3,1),∴-
| -6b2 |
| 2a2 |
∵2c=4
| 6 |
| 6 |
又a2=b2+c2 ③,
联立①②③得:a2=36,b2=12.
∴椭圆的方程为
| x2 |
| 36 |
| y2 |
| 12 |
点评:本题考查了直线与椭圆的关系,训练了点差法求与中点弦有关的问题,考查了学生的计算能力,是中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知函数f(x)=
,若f(x0)=3,则x0的值为( )
|
| A、x0=0 |
| B、x0=8 |
| C、x0=8或x0=0 |
| D、x0=6或x0=0 |
在具有如图所示的正视图和俯视图的几何体中,体积最小的几何体的表面积为 ( )
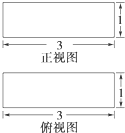

| A、13 | ||
B、7+3
| ||
C、
| ||
| D、14 |
函数f(x)=1-
在其定义域上是( )
| 2 |
| 2x+1 |
| A、单调递增的奇函数 |
| B、单调递增的减函数 |
| C、偶函数且在(0,+∞)上单调递增 |
| D、偶函数且在(0,+∞)上单调递减 |
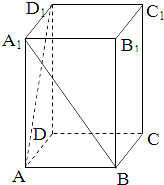 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与D1A所成角的余弦值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.