题目内容
一堆产品中有3个正品(记为a,b,c)和4个次品(记为1,2,3,4),任意抽取2个.
(1)请列出所有基本事件;
(2)记事件A为“恰有一件次品”,事件B为“恰有两件次品”,求P(A∪B);
(3)记事件C为“全都是正品”,求P(C).
(1)请列出所有基本事件;
(2)记事件A为“恰有一件次品”,事件B为“恰有两件次品”,求P(A∪B);
(3)记事件C为“全都是正品”,求P(C).
考点:相互独立事件,古典概型及其概率计算公式
专题:概率与统计
分析:(1)一堆产品中有3个正品(记为a,b,c)和4个次品(记为1,2,3,4),任意抽取2个,所有基本事件为C
=21个,利用列举法能列出所有基本事件.
(2)事件A为“恰有一件次品”,利用等可能事件概率计算公式和互斥事件概率计算公式能求出P(A∪B).
(3)记事件C为“全都是正品”,利用等可能事件概率计算公式能求出P(C).
| C | 2 7 |
(2)事件A为“恰有一件次品”,利用等可能事件概率计算公式和互斥事件概率计算公式能求出P(A∪B).
(3)记事件C为“全都是正品”,利用等可能事件概率计算公式能求出P(C).
解答:
解:(1)一堆产品中有3个正品(记为a,b,c)和4个次品(记为1,2,3,4),
任意抽取2个,所有基本事件为:
(a,b),(a,c),(a,1),(a,2),(a,3),(a,4),(b,c),
(b,1),(b,2),(b,3),(b,4),(c,1),(c,2),(c,3),
(c,4),(1,2),(1,3),(1,4),(2,3),(2,3),(3,4),共21个.
(2)事件A为“恰有一件次品”,
则P(A)=
=
,
事件B为“恰有两件次品”,
则P(B)=
=
,
∴P(A∪B)=
+
=
.
(3)记事件C为“全都是正品”,
则P(C)=
=
.
任意抽取2个,所有基本事件为:
(a,b),(a,c),(a,1),(a,2),(a,3),(a,4),(b,c),
(b,1),(b,2),(b,3),(b,4),(c,1),(c,2),(c,3),
(c,4),(1,2),(1,3),(1,4),(2,3),(2,3),(3,4),共21个.
(2)事件A为“恰有一件次品”,
则P(A)=
| ||||
|
| 4 |
| 7 |
事件B为“恰有两件次品”,
则P(B)=
| ||
|
| 2 |
| 7 |
∴P(A∪B)=
| 4 |
| 7 |
| 2 |
| 7 |
| 6 |
| 7 |
(3)记事件C为“全都是正品”,
则P(C)=
| ||
|
| 1 |
| 7 |
点评:本题考查概率的求法,是基础题,解题时要注意等可能概率计算公式的合理运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
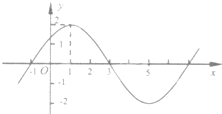 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD.求证:平面PDC⊥平面PAD.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD.求证:平面PDC⊥平面PAD. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.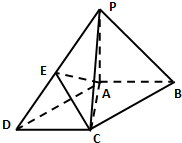 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥面ABCD,AP=AB=3,AD=5,点E是PD的中点.