题目内容
19.若函数$f(x)=\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R,则a的取值范围是( )| A. | (-4,0] | B. | (-4,0) | C. | (0,4] | D. | [0,4) |
分析 由椭圆可知,对任意实数x,ax2-ax+1>0恒成立,然后分a=0和a≠0讨论,当a≠0时,利用二次函数的开口方向和判别式求解.
解答 解:∵函数$f(x)=\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R,
∴对任意实数x,ax2-ax+1>0恒成立,
当a=0时,满足题意;
当a≠0时,需$\left\{\begin{array}{l}{a>0}\\{(-a)^{2}-4a<0}\end{array}\right.$,即0<a<4.
综上,a的取值范围是[0,4).
故选:D.
点评 本题考查函数的定义域及其求法,考查了恒成立问题,体现了分类讨论的数学思想方法,是基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
9.函数y=log2x+3的值域是( )
| A. | [2,+∞) | B. | (3,+∞) | C. | [3,+∞) | D. | (-∞,+∞) |
7.p:x2-3x+2≤0成立的一个必要不充分条件是( )
| A. | x>1 | B. | x≥1 | C. | 1≤x≤2 | D. | 1<x<2 |
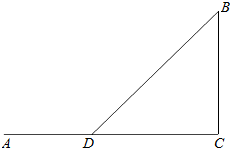 如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.
如图,从海岸线上的港口A到海上油井B要铺设一条石油运输管道,B离海岸线的最近点C为10海里,C和A的距离为10$\sqrt{3}$海里,已知在海岸线上铺设石油管道的价格为a元/海里,在海底铺设石油管道的价格为2a元/海里.在海岸AC上选点D,先在AC上选点D,先在海岸上铺设石油管道AD,再在海底铺设石油管道BD,设铺设石油管道的总费用为y元.