题目内容
9.己知函数f(x)=k3-x-3x是定义域为R的奇函数.(1)求实数k值;
(2)试判断f(x)单调性,并求使不等式f(x2+tx)+f(4-x)>0对任意x∈(1,2)都成立的实数t的取值范围.
分析 (1)根据函数奇偶性的性质,利用f(0)=0进行求解即可.
(2)求出函数的解析式,结合指数函数的单调性进行判断,利用函数奇偶性和单调性的关系将不等式进行转化,构造二次函数,利用根的分布建立不等式关系进行求解即可.
解答 解:(1)∵函数的定义域是(-∞,+∞),
∴若f(x)是奇函数,则f(0)=0,即f(0)=k•30-30=k-1=0,
则k=1.
(2)∵k=1,∴f(x)=3-x-3x,
∵y=3-x是减函数,y=3x是增函数,
∴f(x)=3-x-3x是减函数,
则不等式f(x2+tx)+f(4-x)>0等价为f(x2+tx)>-f(4-x)=f(x-4)对任意x∈(1,2)都成立,
即x2+tx<x-4,对任意x∈(1,2)都成立,
则x2+(t-1)x+4<0,对任意x∈(1,2)都成立,
设g(x)=x2+(t-1)x+4,
则等价为$\left\{\begin{array}{l}{g(1)≤0}\\{g(2)≤0}\\{-\frac{t-1}{2}>0}\end{array}\right.$,即$\left\{\begin{array}{l}{t+4≤0}\\{6+2t≤0}\\{t-1<0}\end{array}\right.$,即$\left\{\begin{array}{l}{t≤-4}\\{t≤-3}\\{t<1}\end{array}\right.$,
即t≤-4.
点评 本题主要考查函数奇偶性的性质以及不等式恒成立问题,根据条件构造一元二次函数,利用根的分布与不等式之间的关系是解决本题的关键.

练习册系列答案
相关题目
19.若函数$f(x)=\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R,则a的取值范围是( )
| A. | (-4,0] | B. | (-4,0) | C. | (0,4] | D. | [0,4) |
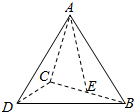 三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC,求证:AE⊥BD.
三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC,求证:AE⊥BD.