题目内容
4.计算(1)log2$\sqrt{\frac{7}{12}}$+log26-$\frac{1}{2}$log228
(2)log${\;}_{\sqrt{2}}$2+log927+$\frac{1}{4}$log4$\frac{1}{16}$+2${\;}^{1+lo{g}_{2}9}$.
分析 (1)利用对数性质、运算法则求解.
(2)利用对数性质、运算法则求解.
解答 解:(1)${log_2}\sqrt{\frac{7}{72}}+{log_2}6-\frac{1}{2}{log_2}28$
=${log}_{2}(\sqrt{\frac{7}{72}}×6÷\sqrt{28})$
=$lo{g}_{2}\sqrt{\frac{1}{8}}$
=$lo{g}_{2}{2}^{-\frac{3}{2}}$
=-$\frac{3}{2}$.
(2)log${\;}_{\sqrt{2}}$2+log927+$\frac{1}{4}$log4$\frac{1}{16}$+2${\;}^{1+lo{g}_{2}9}$
=2+$\frac{3}{2}$-$\frac{1}{2}$+18
=21.
点评 本题考查对数式化简求值,是基础题,解题时要认真审题,注意对数性质、运算法则的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.若函数f(x)=ax-1+1(a>0且a≠1)的反函数恒过定点( )
| A. | (0,2) | B. | (2,0) | C. | (1,2) | D. | (2,1) |
19.若函数$f(x)=\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R,则a的取值范围是( )
| A. | (-4,0] | B. | (-4,0) | C. | (0,4] | D. | [0,4) |
16.某校有高中生900名,其中高一年级300人,高二年级200人,高三年级400人,用分层抽样的方法抽取一个容量为45的样本,则高三年级应抽取( )
| A. | 25人 | B. | 15 人 | C. | 30 人 | D. | 20人 |
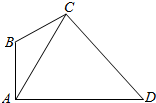 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.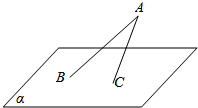 如图,平面α的斜线AB交α于B点,且与α所成角为θ,平面α内一动点C满足∠BAC=$\frac{π}{6}$,若动点C的轨迹为椭圆,则θ的取值范围是$\frac{π}{6}$<θ<$\frac{π}{2}$.
如图,平面α的斜线AB交α于B点,且与α所成角为θ,平面α内一动点C满足∠BAC=$\frac{π}{6}$,若动点C的轨迹为椭圆,则θ的取值范围是$\frac{π}{6}$<θ<$\frac{π}{2}$.