题目内容
11.设全集A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}.(1)若A∩B={0}时,求实数a的值;
(2)如果A∩B=B,求实数a的取值范围.
分析 (1)直接将元素0代入集合B即可求得实数a的值;
(2)先由题设条件求出集合A,再由A∩B=B,导出集合B的可能结果,然后结合根的判别式确定实数a的取值范围.
解答 解:(1)由题意得A={0,-4},
由A∩B={0}得,x=0是方程x2+2(a+1)x+a2-1=0的一个根,
所以,a=1或a=-1;
当a=1时,B={0,-4},不合题意;
当a=-1时,B={0},符合题意;故a=-1.
(2)∵A∩B=B,∴B⊆A,对集合B分类讨论如下:
①当B=∅时,即方程x2+2(a+1)x+a2-1=0无实根,
所以,△=[2(a+1)]2-4(a2-1)=8a+8<0,
解得,a<-1,符合题意;
②当B只含一个元素时,即方程x2+2(a+1)x+a2-1=0有两相等实根,
所以,△=0,解得a=-1,此时,方程为x2=0,
因此,B={0},符合题意;
③当B含两元素时,即B=A={0,-4},此时A,B对应的方程同解,
所以,$\left\{\begin{array}{l}{2(a+1)=4}\\{a^2-1=0}\end{array}\right.$,解得a=1,
综合以上讨论得,实数a的取值范围为:(-∞,-1]∪{1}.
点评 本题主要考查了集合的包含关系的判断和应用,元素与集合的关系,方程根的讨论,体现了分类讨论思想,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.若0<x<y<1,则( )
| A. | 3y<3x | B. | x0.5<y0.5 | C. | logx3<logy3 | D. | log0.5x<log0.5y |
19.若函数$f(x)=\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R,则a的取值范围是( )
| A. | (-4,0] | B. | (-4,0) | C. | (0,4] | D. | [0,4) |
6.下列说法错误的是( )
| A. | 命题“若x2-4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2-4x+3≠0” | |
| B. | “x>1”是“|x|>0”的充分不必要条件 | |
| C. | 若p且q为假命题,则p,q至少有一个假命题 | |
| D. | 命题p:“存在x∈R使得x2+x+1<0,”则¬p:“对于任意x∈R,均有x2+x+1>0” |
16.某校有高中生900名,其中高一年级300人,高二年级200人,高三年级400人,用分层抽样的方法抽取一个容量为45的样本,则高三年级应抽取( )
| A. | 25人 | B. | 15 人 | C. | 30 人 | D. | 20人 |
3.已知直线3x+2y-3=0与6x+my+7=0互相平行,则它们之间的距离是( )
| A. | 4 | B. | $\frac{{\sqrt{13}}}{2}$ | C. | $\frac{{2\sqrt{13}}}{13}$ | D. | $\frac{{7\sqrt{13}}}{26}$ |
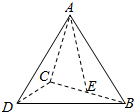 三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC,求证:AE⊥BD.
三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC,求证:AE⊥BD.