题目内容
18．
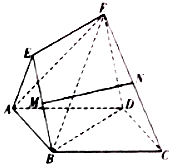如图5所示，四边形ABCD是边长为2的正方形，四边形BDFE是平行四边形，点M，N分别是BE，CF的中点．（1）求证：MN∥平面ABCD；
（2）若△ABE是等边三角形且平面ABE⊥平面ABCD，记三棱柱E-ABF的体积为S1，四棱锥F-ABCD的体积为S2，求$\frac{S_1}{S_2}$的值．
分析 （1）取DF的中点H，连接MH，NH，推导出NH∥CD．MH∥BD，从而平面MNH∥平面ABCD，由此能证明MN∥平面ABCD．
（2）推导出DF∥平面ABE，从而S1=VE-ABF=VF-ABE=VD-ABE=VE-ABD，推导出EF∥平面ABCD，从而S2=VF-ABCD=VE-ABCD=2VE-ABD=2S1，由此能求出结果．
解答 证明：（1）如图，取DF的中点H，连接MH，NH，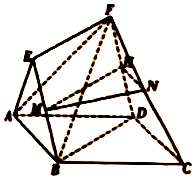
∵点N，H分别是CF，DF的中点，∴NH∥CD．
∵EBDF是平行四边形，且点M，H是BE，DF的中点，∴MH∥BD，
又MH∩NH=H，BD∩CD=D，∴平面MNH∥平面ABCD，
又∵MN?平面MNH，∴MN∥平面ABCD．
解：（2）∵DF∥BE，DF?平面ABE，BE?平面ABE，
∴DF∥平面ABE，
∴S1=VE-ABF=VF-ABE=VD-ABE=VE-ABD，
又EF∥BD，EF?平面ABCD，BD?平面ABCD，
∴EF∥平面ABCD，
∴S2=VF-ABCD=VE-ABCD=2VE-ABD=2S1，
∴$\frac{S_1}{S_2}=\frac{1}{2}$．
点评 本题考查线面垂直的证明，考查三棱柱与四棱锥的体积之比的求法，是中档题，解题时要认真审题，注意等体积法的合理运用．
练习册系列答案
相关题目
8．在等差数列{an}中，a1=3，2a2=a4，则a7等于（ ）
| A． | 12 | B． | 15 | C． | 18 | D． | 21 |
9．若a=log0.60.3，b=0.60.3，则（ ）
| A． | a＞1＞b | B． | a＞b＞1 | C． | b＞a＞1 | D． | b＞1＞a |
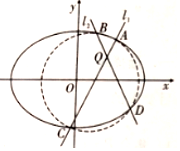已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞1}）$中，a=$\sqrt{2}$b，且椭圆E上任一点到点$P（{-\frac{1}{2}，0}）$的最小距离为$\frac{{\sqrt{7}}}{2}$．
10．在正项等比数列{an}中，a3=2，a4=8a7，则a9=（ ）
| A． | $\frac{1}{256}$ | B． | $\frac{1}{128}$ | C． | $\frac{1}{64}$ | D． | $\frac{1}{32}$ |