题目内容
5.下列说法中正确的是( )| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | “|a|>|b|”与“a2>b2”不等价. | |
| C. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0”. | |
| D. | 一个命题的否命题为真,则它的逆命题一定为真. |
分析 利用四种命题的真假关系判断A的正误;不等式的等价性判断B的正误;逆否命题的形式判断C的正误;利用四种命题的真假关系判断D的正误.
解答 解:对于A:一个命题的逆命题为真,则它的否命题一定为真,但是逆否命题不能判断真假;所以A不正确;
对于B:“|a|>|b|”与“a2>b2”是等价不等式,所以B不正确;
对于C:“a2+b2=0,则a,b全为0”的逆否命题是“若a,b不全为0,则a2+b2≠0”,不是“若a,b全不为0,则a2+b2≠0”,所以C不正确;
对于D:一个命题的否命题为真,则它的逆命题一定为真,满足四种命题的真假关系,正确;
故选:D.
点评 本题考查命题的真假的判断与应用,是基本知识的考查.

练习册系列答案
相关题目
15.设A={(x,y)|y=cos(arccosx)},B={(x,y)|y=arccos(cosx)},则A∩B=( )
| A. | {(x,y)|y=x,-1≤x≤1} | B. | $\left\{{(x\;,\;\;y)\left|{y=x\;,\;\;-\frac{1}{2}≤x≤\frac{1}{2}}\right.}\right\}$ | ||
| C. | {(x,y)y=x,0≤x≤1} | D. | {(x,y)|y=x,0≤x≤π} |
16.已知椭圆E的左、右焦点分别为F1,F2,过F1且斜率为2的直线交椭圆E于P,Q两点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,则椭圆E的离心率为( )
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
17.下列函数中,图象的一部分如右图所示的是( )
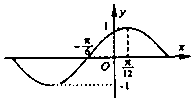

| A. | $y=sin({x+\frac{π}{6}})$ | B. | $y=cos({2x-\frac{π}{6}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({4x-\frac{π}{3}})$ |
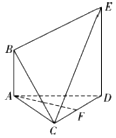 如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点.
如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点. 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.