题目内容
8.一厂家生产A、B、C三类空气净化器,每类净化器均有经典版和至尊版两种型号,某月的产量如表(单位:台):| 空气净化器A | 空气净化器B | 空气净化器C | |
| 经典版 | 100 | 150 | 400 |
| 至尊版 | 300 | 450 | 600 |
(Ⅱ)用随机抽样的方法从B类空气净化器中抽取8台,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8台空气净化器的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
分析 (Ⅰ)求出5台中2台经典版,3台至尊版,根据满足条件的概率即可;
(Ⅱ)求出8个数据的平均数,作差,求出满足条件的数据的个数,从而求出满足条件的概率即可.
解答 解:(Ⅰ)$\frac{4}{10}$×5=2,$\frac{6}{10}$×5=3,
故5台中2台经典版,3台至尊版,
故满足条件的概率是:p=$\frac{{{C}_{2}^{1}C}_{3}^{1}{+C}_{2}^{2}}{{C}_{5}^{2}}$=0.7;
(Ⅱ)设9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2的平均数是$\overline{x}$,
则$\overline{x}$=9,
则该数与样本平均数之差的绝对值不超过0.5的共6个,
满足条件的概率是p=$\frac{6}{8}$=$\frac{3}{4}$.
点评 本题考查了条件概率问题,考查平均数问题,是一道基础题.

练习册系列答案
相关题目
19.若a,b∈{-1,1,2,3},则直线ax+by=0与圆x2+(y+2)2=2有交点的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{11}{16}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{16}$ |
16.已知集合M={x|16-x2≥0},集合N={y|y=|x|+1},则M∩N=( )
| A. | {x|-2≤x≤4} | B. | {x|x≥1} | C. | {x|1≤x≤4} | D. | {x|x≥-2} |
13.函数f(x)=ln(4-x)的定义域为( )
| A. | (-∞,4] | B. | (-∞,4) | C. | (0,4] | D. | (0,4) |
20.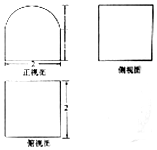 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )| A. | 12+3π | B. | 10+3π | C. | 12+4π | D. | 10+4π |
17.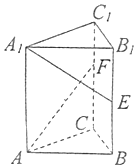 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )| A. | $-\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{6}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
18.已知a,b是两条不同的直线,α是平面,且b?α,那么“a∥α”是“a∥b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
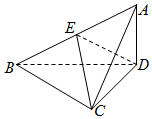 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.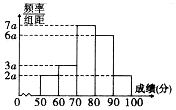 在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.
在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.