题目内容
18.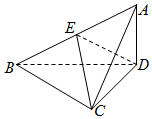 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
分析 (1)由AD⊥平面BCD,可得AD⊥BC,又AC⊥BC,可得BC⊥平面ACD,即可证明平面ABC⊥平面ACD.
(2)由已知可得$CD=\sqrt{3}$,取CD中点为F,连接EF,利用直角三角形斜边中线的性质可得:△ECD为等腰三角形,由(1)知BC⊥平面ACD,可得点E到平面ACD的距离为1,令A到平面CED的距离为d,则${V_{A-ECD}}=\frac{1}{3}•{S_{△ECD}}•d={V_{E-ACD}}=\frac{1}{3}•{S_{△ACD}}•1$,解得d.
解答 (1)证明:∵AD⊥平面BCD,BC?平面BCD,∴AD⊥BC,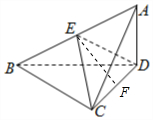
又∵AC⊥BC,AC∩AD=A,∴BC⊥平面ACD,BC?平面ABC,
∴平面ABC⊥平面ACD.(6分)
(2)解:由已知可得$CD=\sqrt{3}$,取CD中点为F,连接EF,
∵$ED=EC=\frac{1}{2}AB=\sqrt{2}$,∴△ECD为等腰三角形,
从而$EF=\frac{{\sqrt{5}}}{2}$,${S_{△ECD}}=\frac{{\sqrt{15}}}{4}$,
由(1)知BC⊥平面ACD,∴点E到平面ACD的距离为1,${S_{△ACD}}=\frac{{\sqrt{3}}}{2}$,
令A到平面CED的距离为d,则${V_{A-ECD}}=\frac{1}{3}•{S_{△ECD}}•d={V_{E-ACD}}=\frac{1}{3}•{S_{△ACD}}•1$,解得$d=\frac{{2\sqrt{5}}}{5}$.(12分)
点评 本题考查了线面面面垂直、求点到平面距离问题等,本题考查了学生的空间想象能力、推理论证能力和运算求解能力,属于中档题.

练习册系列答案
相关题目
3.将函数y=sin(x+$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{4}$个的单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得图象的解析式为( )
| A. | y=sin(2x+$\frac{5π}{12}$) | B. | y=sin($\frac{x}{2}$+$\frac{5π}{12}$) | C. | y=sin ($\frac{x}{2}$-$\frac{π}{12}$) | D. | y=sin($\frac{x}{2}$+$\frac{5π}{24}$) |
8.一厂家生产A、B、C三类空气净化器,每类净化器均有经典版和至尊版两种型号,某月的产量如表(单位:台):
(I)在C类空气净化器中,用分层抽样的方法抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1台经典版空气净化器的概率;
(Ⅱ)用随机抽样的方法从B类空气净化器中抽取8台,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8台空气净化器的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
| 空气净化器A | 空气净化器B | 空气净化器C | |
| 经典版 | 100 | 150 | 400 |
| 至尊版 | 300 | 450 | 600 |
(Ⅱ)用随机抽样的方法从B类空气净化器中抽取8台,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8台空气净化器的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
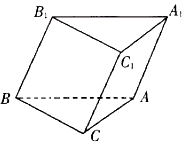 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2. 在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,$∠DAB=\frac{π}{3}$,AB=2,AM=1,E是AB的中点.
在如图所示的几何体中,平面ADNM⊥平面ABCD,四边形ABCD是菱形,ADNM是矩形,$∠DAB=\frac{π}{3}$,AB=2,AM=1,E是AB的中点.