题目内容
16.已知双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1,则其渐近线方程为( )| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±$\frac{1}{3}$x | D. | y=±3x |
分析 根据题意,由双曲线的标准方程可得其焦点在x轴上,且a=$\sqrt{12}$=2$\sqrt{3}$,b=$\sqrt{4}$=2,将a、b的值代入焦点在x轴上的双曲线的渐近线方程计算可得答案.
解答 解:根据题意,双曲线的标准方程为:$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1,
则其焦点在x轴上,且a=$\sqrt{12}$=2$\sqrt{3}$,b=$\sqrt{4}$=2,
故其渐近线方程为y=±$\frac{\sqrt{3}}{3}$x;
故选:A.
点评 本题考查双曲线的集合性质,注意分析双曲线的标准方程的形式,确定其焦点的位置.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
6.如果函数f(x)=(a2-1)x在R上是减函数,那么实数a的取值范围是( )
| A. | |a|>1 | B. | |a|<2 | C. | |a|>3 | D. | 1<|a|<$\sqrt{2}$ |
7.集合A={1,2}的非空子集个数为( )
| A. | 4 | B. | 2 | C. | 1 | D. | 3 |
4.一个几何体的三视图如图所示,则该几何体的表面积是( )
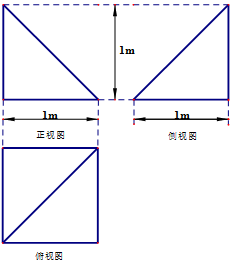

| A. | $(1+\sqrt{2}){m^2}$ | B. | $(1+2\sqrt{2}){m^2}$ | C. | $(2+\sqrt{2}){m^2}$ | D. | $(2+2\sqrt{2}){m^2}$ |
1.已知球O的内接圆柱的体积是2π,底面半径为1,则球O的表面积为( )
| A. | 6π | B. | 8π | C. | 10π | D. | 12π |
8.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>b>0)的一条渐近线方程为y=$\frac{1}{2}$x,则其离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 2$\sqrt{2}$ |
5.在等差数列{an}中,a1=-6,公差为d,前n项和为Sn,当且仅当n=6时,Sn取得最小值,则d的取值范围为( )
| A. | $(-1,-\frac{7}{8})$ | B. | (0,+∞) | C. | (-∞,0) | D. | $(1,\frac{6}{5})$ |