题目内容
5.已知△ABC中A(1,0),B(4,0),C(2,5)(1)求AC边上的高线方程
(2)求BC边上的中线方程.
分析 (1)由题意和斜率可得kAC=5,由垂直关系可得高线的斜率为-$\frac{1}{5}$,可得高线方程;
(2)由中点公式可得BC中点D(3,$\frac{5}{2}$),可得中线AD的斜率,可得方程.
解答 解:(1)∵△ABC中A(1,0),B(4,0),C(2,5),
∴kAC=$\frac{5-0}{2-1}$=5,故高线的斜率为-$\frac{1}{5}$,
∴高线方程为y-0=-$\frac{1}{5}$(x-4),
整理为一般式可得x+5y-4=0;
(2)由中点公式可得BC中点D(3,$\frac{5}{2}$),
∴中线AD的斜率为$\frac{\frac{5}{2}-0}{3-1}$=$\frac{5}{4}$,
∴BC边上的中线AD方程为y-0=$\frac{5}{4}$(x-1),
整理为一般式可得5x-4y-5=0.
点评 本题考查直线的一般式方程和垂直关系,涉及斜率公式和中点坐标公式,属基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
20.空间直角坐标系中点P(1,2,3)关于y轴的对称点的坐标为( )
| A. | (3,2,1) | B. | (1,-2,3) | C. | (-1,2,-3) | D. | (1,2,3) |
15.已知集合A={x2-5x-6<0},B={x|2x<1},则图中阴影部分表示的集合是( )
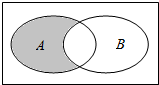

| A. | {x|2<x<3} | B. | {x|-1<x≤0} | C. | {x|0≤x<6} | D. | {x|x<-1} |