题目内容
14.若y=x2+(log2N)x+log2N的最小值为$\frac{3}{4}$,求N.分析 配方法化简y=(x+$\frac{lo{g}_{2}N}{2}$)2+log2N-$\frac{(-lo{g}_{2}N)^{2}}{4}$,从而可得$\frac{(-lo{g}_{2}N)^{2}}{4}$-log2N•$\frac{lo{g}_{2}N}{2}$+log2N=$\frac{3}{4}$,从而解得.
解答 解:y=x2+(log2N)x+log2N
=(x+$\frac{lo{g}_{2}N}{2}$)2+log2N-$\frac{(-lo{g}_{2}N)^{2}}{4}$,
故当x=-$\frac{lo{g}_{2}N}{2}$时有最小值,
即ymin=$\frac{(-lo{g}_{2}N)^{2}}{4}$-log2N•$\frac{lo{g}_{2}N}{2}$+log2N=$\frac{3}{4}$,
解得,log2N=1或log2N=3,
即N=2或N=8.
点评 本题考查了配方法及整体的思想应用,关键在于将log2N看成一个整体,从而化简并解方程,从而解得.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.在由一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的点所构成的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-2x+1上,则这组样本数据中变量x,y的相关系数为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
2.设f(x)=2+5x+10x2+10x3+5x4+x5,则其反函数的解析式为( )
| A. | $y=1+\root{5}{x-1}$ | B. | $y=1-\root{5}{x-1}$ | C. | $y=-1+\root{5}{x-1}$ | D. | $y=-1-\root{5}{x-1}$ |
6.已知直三棱柱A1B1C1-ABC的三视图如图所示,D,E分别是棱CC1和棱B1C1的中点,则三棱锥E-ABD的体积为( )
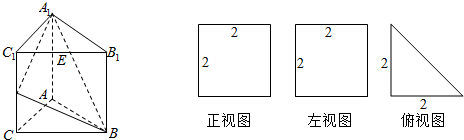

| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 3 | D. | 1 |
3.已知函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,函数g(x)=f[f(x)]-$\frac{1}{2}$的三个零点为x1,x2,x3,且x1<x2<x3,则( )
| A. | x2+x3=$\frac{3}{4}$ | B. | x2+x3=1 | C. | x1+x2=$\frac{1}{4}$ | D. | x1+x2=-$\frac{1}{4}$ |
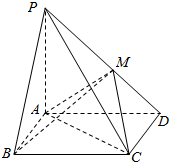 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.求直线BM与平面ACM所成的角的正弦值.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.求直线BM与平面ACM所成的角的正弦值.