题目内容
14.已知z1与z2是共轭虚数,有4个命题①z12<|z2|2; ②z1z2=|z1z2|;③z1+z2∈R;④$\frac{{z}_{1}}{{z}_{2}}$∈R,一定正确的是( )| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
分析 z1与z2是共轭虚数,设z1=a+bi(a,b∈R),z2=a-bi.利用复数的运算性质及其有关概念即可得出.
解答 解:z1与z2是共轭虚数,设z1=a+bi,z2=a-bi(a,b∈R).
命题①z12<|z2|2; ${z}_{1}^{2}$=a2-b2+2abi,复数不能比较大小,因此不正确;
②z1z2=|z1z2|=a2+b2,正确;
③z1+z2=2a∈R,正确;
④$\frac{{z}_{1}}{{z}_{2}}$=$\frac{a+bi}{a-bi}$=$\frac{(a+bi)^{2}}{(a-bi)(a+bi)}$=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$+$\frac{2ab}{{a}^{2}+{b}^{2}}$i不一定是实数,因此不一定正确.
故选:B.
点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如图是一个正方体被切掉部分后所得几何体的三视图,则该几何体的体积为( )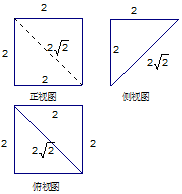

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
5.若关于x的方程x2-xlnx+2=k(x+2)在[$\frac{1}{2}$,+∞)上有两解,则实数k的取值范围为( )
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
2.若0<x1<x2<1,则( )
| A. | ex2-ex1>lnx2-lnx1 | B. | ex2-ex1<lnx2-lnx1 | ||
| C. | x2ex1>x1ex2 | D. | x2ex1<x1ex2 |
6.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知函数f(x)=-x2-6x-3,g(x)=2x3+3x2-12x+9,m<-2,若?x1∈[m,-2),?x2∈(0,+∞),使得f(x1)=g(x2)成立,则m的最小值为( )
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |