题目内容

9．设数列{an}是各项为正数的等比数列，Sn为其前n项和，已知a2a4=16，$\frac{{a}_{4}+{a}_{5}+{a}_{8}}{{a}_{1}+{a}_{2}+{a}_{5}}$=8，则S5=（　　）
A．40B．20C．31D．43

分析 利用等比数列的通项公式及其性质即可得出．

解答 解：设等比数列{an}的公比为q＞0，∵a2a4=16，$\frac{{a}_{4}+{a}_{5}+{a}_{8}}{{a}_{1}+{a}_{2}+{a}_{5}}$=8，
∴${a}_{1}^{2}{q}^{4}$=16，q3=8，解得q=2，a1=1．
则S5=$\frac{{2}^{5}-1}{2-1}$=31．
故选：C．

点评 本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
19．已知实数x，y满足$\left\{\begin{array}{l}{x-2y≥0}\\{x-y-1≤0}\\{y＞0}\end{array}\right.$，且z=$\frac{2x+y}{\sqrt{{x}^{2}+{y}^{2}}}$的最大值为$\sqrt{5}$．
20．设集合A={x∈R|x-1＞0}，B={x∈R|x＜0}，C={x∈R|x（x-2）＞0}，则“x∈A∪B“是“x∈C“的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
17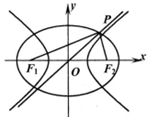．如图，点F1、F2是椭圆C1、C2的左右焦点，椭圆C1与双曲线C2的渐近线交于点P，PF1⊥PF2，椭圆C1与双曲线C2的离心率分别为e1、e2，则（　　）
A．e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$B．e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$
C．e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$D．e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$
4．若数列{an}满足：只要ap=aq（p，q∈N*），必有ap+1=aq+1，那么就称数列{an}具有相纸P，已知数列{an}具有性质P，且a1=1，a2=2，a3=3，a5=2，a6+a7+a8=21，则a2017=15．
14．在直角坐标系xoy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=2+2sinθ}\end{array}\right.$（θ为参数），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系．
（Ⅰ）写出曲线C的极坐标方程；
（Ⅱ）设点M的极坐标为（$\sqrt{2}$，$\frac{π}{4}$），过点M的直线l与曲线C相交于A，B两点，求|MA|•|MB|
1．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$与直线y=x+3只有一个公共点，且椭圆的离心率为$\frac{{\sqrt{5}}}{5}$，则椭圆C的方程为（　　）
A．$\frac{x^2}{16}+\frac{y^2}{9}=1$B．$\frac{x^2}{5}+\frac{y^2}{4}=1$C．$\frac{x^2}{9}+\frac{y^2}{5}=1$D．$\frac{x^2}{25}+\frac{y^2}{20}=1$
18．《九章算术》有这样一个问题：今有女子善织，日增等尺，第二日、第五日、第八日所织之和为十五尺，九日共织尺数是（　　）
A．5B．15C．45D．10
19．已知定义域为R的函数$f（x）=\frac{{a-{3^x}}}{{{3^x}+1}}$是奇函数．
（1）求a的值；      
（2）证明f（x）在（-∞，+∞）上为减函数；      
（3）若对于任意$x∈[{-\frac{π}{6}，\frac{π}{3}}]$，不等式f（sin2x）+f（2-k）＜0恒成立，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网