题目内容
9.若an是(2+x)n(n∈N*,n≥2,x∈R)展开式中x2项的二项式系数,则$\lim_{n→∞}(\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{a_n})$=2.分析 (2+x)n(其中n=2,3,4,…)的展开式,Tr+1,令r=2,可得an,再利用求和公式化简,利用数列的极限即可得出.
解答 解:(2+x)n(其中n=2,3,4,…)的展开式,Tr+1=${C}_{n}^{r}{2}^{n-r}{x}^{r}$,令r=2,可得:T3=2n-2${C}_{n}^{2}$x2.
∴an是二项式(2+x)n(其中n=2,3,4,…)的展开式中x的二项式系数,
∴an=${C}_{n}^{2}$=$\frac{n(n-1)}{2}$.
则$\lim_{n→∞}(\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{a_n})$=$\underset{lim}{n→∞}$2$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n-1}-\frac{1}{n})$=$\underset{lim}{n→∞}$$(2-\frac{2}{n})$=2.
故答案为:2.
点评 本题考查二项式定理的应用,数列求和,数列的极限的求法,考查计算能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
19.已知复数z=x+yi(x,y∈R)满足$|{\overline z}|≤1$,则y≥x-1的概率为( )
| A. | $\frac{3}{4}-\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{3}{4}+\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
8.已知函数f(x)=x2-3x+c,(x∈[1,3]的值域为( )
| A. | [f(1),f(3)] | B. | [f(1),f($\frac{3}{2}$)] | C. | [c-$\frac{9}{4}$,f(3)] | D. | [f($\frac{3}{2}$),f(3)] |
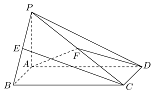 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与