题目内容
1.已知数列{an}的前n项和为${S_n}={2^n}-1$,则此数列的通项公式为an=2n-1.分析 根据题意和公式${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,化简后求出数列的通项公式
解答 解:当n=1时,a1=S1=2-1=1,
当n≥2时,an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1,
又21-1=1,所以an=2n-1,
故答案为:an=2n-1.
点评 本题考查了an、Sn的关系式:${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$的应用,注意验证n=1是否成立.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
12.设x∈R,则“x<-2”是“x2+x≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
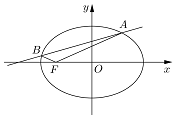 已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;