题目内容
11.若x、y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{y≤x}\\{y≥1}\end{array}\right.$,z=ax+y最大时的最优解有无数个,则a=±1.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,结合题意可知,当直线y=-ax+z与两直线y=x或x+y=4重合时,使目标函数z=ax+y取得最大值的最优解有无数个,由此可得a的值.
解答 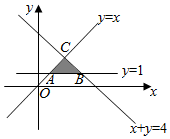 解:由约束条件$\left\{\begin{array}{l}{x+y≤4}\\{y≤x}\\{y≥1}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{x+y≤4}\\{y≤x}\\{y≥1}\end{array}\right.$作出可行域如图,
化目标函数z=ax+y为y=-ax+z.
由图可知,当直线y=-ax+z与两直线y=x或x+y=4重合时,
使目标函数z=ax+y取得最大值的最优解有无数个,
∴a=±1.
故答案为:±1.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
1.若双曲线$\frac{x^2}{a^2}-{y^2}=1(a>0)$的一条渐近线与圆x2+(y-2)2=2至多有一个交点,则双曲线离心率的取值范围是( )
| A. | $[\sqrt{2},+∞)$ | B. | [2,+∞) | C. | $({1,\sqrt{2}}]$ | D. | (1,2] |
20.多次执行如图所示的程序框图,输出的$\frac{m}{n}$的值会稳定在某个常数附近,则这个常数为( )


| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
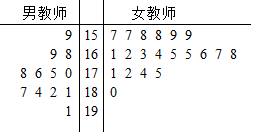 新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.
新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.