在△ABC中.角A.B.C对应的边分别为a.b.c．若a2=(b+c)2-bc.则A$\frac{2π}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

8．在△ABC中，角A，B，C对应的边分别为a，b，c．若a²=（b+c）²-bc，则A$\frac{2π}{3}$．

分析利用余弦定理即可得出．

解答解：在△ABC中，∵a²=（b+c）²-bc，
∴b²+c²-a²=-bc．
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{-bc}{2bc}$=-$\frac{1}{2}$．
A∈（0，π）．
∴A=$\frac{2}{3}π$．
故答案为：$\frac{2π}{3}$．

点评本题考查了余弦定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案

19．已知椭圆C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数），直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=t}\end{array}\right.$（t为参数）．
（1）将直线l与椭圆C的参数方程均化为普通方程；
（2）设直线l与椭圆C的两个交点分别为A，B，求线段AB的长．

16．

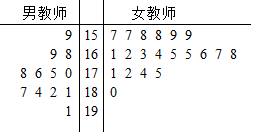新疆某中学共有教师32人，其中男教师12人，女教师20人，这32名教师的身高如下面的茎叶图所示（单位：cm）．为“打击疆独分子，确保学校师生安全”，校委会决定：身高在175cm以上（含175cm）的男教师和身高在172cm以上（含172cm）的女教师组成“校外巡逻队”，其余教师组成“校内巡逻队”．
（1）若用分层抽样的方法从“校外巡逻队员”和“校内巡逻队员”中抽取中选8人，然后在从这8人中选3人，求至少有1人是“校外巡逻队员”的概率；
（2）若从所有“校外巡逻队员”中选2人作为“校外巡逻队”队长，用X表示“校外巡逻队”队长为女教师的人数，试写出X的分布列，并求X的数学期望．

3．若复数z满足：z（3+3i）=1-2i，则z的虚部为$-\frac{1}{2}$．

13．已知等差数列{a_n}的首项a₁=1，公差d＞0，数列{b_n}是等比数列，且b₂=a₂，b₃=a₅，b₄=a₁₄．
（I）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）设数列{c_n}对任意正整数n，均有$\frac{c_1}{b_1}+\frac{c_2}{b_2}+…+\frac{c_n}{b_n}={a_{n+1}}$成立，求c₁+c₂+…+c₂₀₁₄的值．

20．多次执行如图所示的程序框图，输出的$\frac{m}{n}$的值会稳定在某个常数附近，则这个常数为（　　）

17．已知f（x）=|ax-1|（x∈R），不等式f（x）≤3的解集为{x|-2≤x≤1}．
（1）求a的值；
（2）若f（x）-2f（${\frac{x}{2}}$）＞$\frac{-a}{x^2}$+$\frac{k}{2}{x^2}$+k的解集非空，求k的取值范围．

18．己知函数f（x）=$\frac{1}{2}$x²+ln（-x）．数列{x_n}（x_n＜0）的第一项x₁=-$\frac{2}{3}$，其前n项和为S_n，以后各项及S_n均按如下方式给定：曲线y=f（x）在点（S_n，f（S_n））处的切线的斜率为x_n-2（n≥2，n∈N⁺）．
（1）试计算S₁、S₂、S₃、S₄，并由此猜想S_n（只含n）的表达式；
（2）证明（1）的猜想，并求出数列{x_n}的通项．

试题分类