题目内容
设a,b,c都是正实数,且a,b满足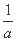 +
+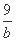 =1,求使a+b≥c恒成立的c的取值范围;
=1,求使a+b≥c恒成立的c的取值范围;
因为a,b,c都是正实数,且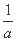 +
+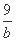 =1,
=1,
所以a+b=(a+b)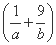 =10+
=10+ +
+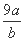 ≥10+2
≥10+2 =16,
=16,
当且仅当 =
=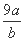 ,即b=3a时等号成立.
,即b=3a时等号成立.
要使a+b≥c恒成立,则0<c≤16,即c的取值范围为(0,16].

练习册系列答案
相关题目
题目内容
设a,b,c都是正实数,且a,b满足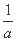 +
+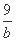 =1,求使a+b≥c恒成立的c的取值范围;
=1,求使a+b≥c恒成立的c的取值范围;
因为a,b,c都是正实数,且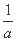 +
+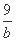 =1,
=1,
所以a+b=(a+b)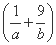 =10+
=10+ +
+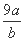 ≥10+2
≥10+2 =16,
=16,
当且仅当 =
=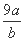 ,即b=3a时等号成立.
,即b=3a时等号成立.
要使a+b≥c恒成立,则0<c≤16,即c的取值范围为(0,16].
