题目内容
已知各项均为正数的数列{an}的前n项和为Sn,满足8Sn= +4an+3(n∈N*),且a1,a2,a7依次是等比数列{bn}的前三项.
+4an+3(n∈N*),且a1,a2,a7依次是等比数列{bn}的前三项.
(1) 求数列{an}及{bn}的通项公式;
(2) 是否存在常数a>0且a≠1,使得数列{an-logabn}(n∈N*)是常数列?若存在,求出a的值;若不存在,说明理由.
(1) 当n=1时,8a1=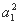 +4a1+3,a1=1或a1=3.
+4a1+3,a1=1或a1=3.
当n≥2时,8Sn-1=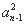 +4an-1+3,an=Sn-Sn-1=
+4an-1+3,an=Sn-Sn-1= (
( +4an-
+4an-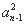 -4an-1),
-4an-1),
从而(an+an-1)(an-an-1-4)=0.
因为{an}各项均为正数,所以an-an-1=4.
所以,当a1=1时,an=4n-3;当a1=3时,an=4n-1.
又因为当a1=1时,a1,a2,a7分别为1,5,25,构成等比数列,
所以an=4n-3,bn=5n-1.
当a1=3时,a1,a2,a7分别为3,7,27,不构成等比数列,舍去.综上,an=4n-3,bn=5n-1.
(2) 由(1)知,an=4n-3,bn=5n-1,从而
an-logabn=4n-3-loga5n-1=4n-3-(n-1)loga5=(4-loga5)n-3+loga5.
由题意,得4-loga5=0,所以a= .所以,满足条件的a存在,a=
.所以,满足条件的a存在,a= .
.

练习册系列答案
相关题目
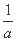 +
+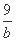 =1,求使a+b≥c恒成立的c的取值范围;
=1,求使a+b≥c恒成立的c的取值范围;
 A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是 .(填序号)
A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是 .(填序号) 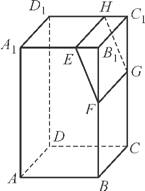
 ,an+1=
,an+1= (n∈N*),用数学归纳法证明:an>2(n∈N*).
(n∈N*),用数学归纳法证明:an>2(n∈N*).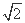 cos
cos ,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为
,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为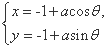 (θ是参数),若圆C1与圆C2相切,求实数a的值.
(θ是参数),若圆C1与圆C2相切,求实数a的值.