题目内容
已知A,B,C是△ABC的三个内角,向量a=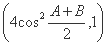 ,b=
,b=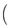 1,2sin2
1,2sin2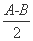 -3
-3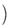 .
.
(1) 若|a|=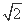 ,求角C的大小;
,求角C的大小;
(2) 若a⊥b,求tanA·tanB的值.
(1) 因为|a|=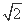 ,所以
,所以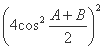 +1=2,
+1=2,
所以4[1+cos(A+B)]2=1.
因为A+B+C=π,所以A+B=π-C.
所以(1-cos C)2=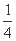 ,所以1-cos C=±
,所以1-cos C=±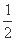 ,cos C=
,cos C=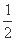 或
或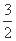 (舍去).因为0<C<π,所以C=
(舍去).因为0<C<π,所以C= .
.
(2) 由a⊥b,得a·b=0,
所以4cos2 +2sin2
+2sin2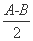 -3=0,
-3=0,
所以2[1+cos(A+B)]+[1-cos(A-B)]-3=0,
所以2cos(A+B)-cos(A-B)=0,
即cos Acos B-3sin Asin B=0,
所以tan A·tan B= .
.

练习册系列答案
相关题目
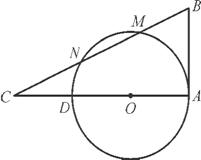
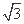 ,则等轴双曲线C的实轴长为 .
,则等轴双曲线C的实轴长为 . 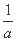 +
+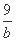 =1,求使a+b≥c恒成立的c的取值范围;
=1,求使a+b≥c恒成立的c的取值范围;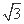 ,c=
,c= ,则最小的内角等于 .
,则最小的内角等于 . 