题目内容
7个人排成一排,在下列情况下,各有多少种不同排法
(1) 甲不在排头,也不在排尾;
(2) 甲、乙之间有且只有2人;
(3) 甲、乙、丙3人两两相邻;
(4)甲在乙的左边(不一定相邻).
(1) 先排甲,有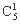
种排法;再排余下的,有
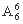种排法.所以共有
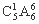=3 600种不同的排法.
(2) 可先排甲、乙,有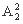
种排法;再在甲与乙插入两人,有
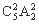种排法;把这4人和余下的3人进行排列,所以共有
=960种不同排法.
(3) 先排甲、乙、丙,有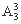
种排法;再把甲、乙、丙看做一个整体与余下的4人做全排列,共有
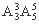=720种不同排法.
(4) 甲在乙左与甲在乙右各占所有情况数的一半,所以甲在乙的左边共有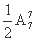
=2 520种不同排法.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
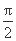时,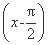
f'(x)>0,则函数y=f(x)-sin x在[-2π,2π]上的零点个数为 . 
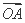=(1,-2),
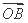=(a,-1),
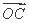=(-b,0),a>0,b>0,O为坐标原点,若A,B,C三点共线,则
+
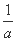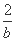的最小值为 . 
+
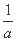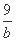=1,求使a+b≥c恒成立的c的取值范围;