题目内容
14. 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC的中点,求AD与平面PAC所成的角的正弦值的大小.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC的中点,求AD与平面PAC所成的角的正弦值的大小.
分析 以A为原点建立空间直角坐标系A-xyz,利用向量法能求出AD与平面PAC所成的角的正弦值.
解答  解:如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,
解:如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,
以A为原点建立空间直角坐标系A-xyz,
设PA=a,由已知可得$A(0,0,0),B(-\frac{a}{2},\frac{{\sqrt{3}}}{2}a,0)$,
$C(0,\frac{{\sqrt{3}}}{2}a,0),P(0,0,a)$,$D(-\frac{a}{4},\frac{{\sqrt{3}a}}{4},\frac{a}{2})$
$\overrightarrow{AP}=(0,0,a)$,$\overrightarrow{BC}$=($\frac{a}{2}$,0,0),
∵$\overrightarrow{AP}=(0,0,a),\overrightarrow{BC}=(\frac{a}{2},0,0)$,∴$\overrightarrow{BC}•\overrightarrow{AP}=0$,∴BC⊥AP.
又∵∠BCA=90°,∴BC⊥AC,∴BC⊥平面PAC.
∴平面PAC的一个法向量$\overrightarrow{BC}=(\frac{a}{2},0,0)$,
设AD与平面PAC所成的角为α,∴$sinα=|{cos<\overrightarrow{AD,}\overrightarrow{BC}>}|=\frac{{\sqrt{2}}}{4}$
∴AD与平面PAC所成的角的正弦值是$\frac{{\sqrt{2}}}{4}$.
点评 本题考查直线与平面所成角的大小的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
9.已知全集U={0,1,2,3,4},M={2,3,4},N={0,1,2,3},则图中阴影部分所表示的集合为( )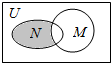

| A. | {2,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1} |
6.已知等差数列{an}的前n项和为Sn,若S21=63,则a11=( )
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
3.已知正三角形ABC的边长为2,D是BC边的中点,将三角形ABC沿AD翻折,使$BC=\sqrt{3}$,若三棱锥A-BCD的四个顶点都在球O的球面上,则球O的表面积为( )
| A. | 7π | B. | 19π | C. | $\frac{{7\sqrt{7}}}{6}π$ | D. | $\frac{{19\sqrt{19}}}{6}π$ |
4.在等比数列{an}中,已知a1=1,a3=2a2,则该数列前6项和S6=( )
| A. | 31 | B. | 63 | C. | 127 | D. | 176 |
 正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
正方体ABCD-A1B1C1D1中,E是棱DD1的中点.