题目内容
3.已知正三角形ABC的边长为2,D是BC边的中点,将三角形ABC沿AD翻折,使$BC=\sqrt{3}$,若三棱锥A-BCD的四个顶点都在球O的球面上,则球O的表面积为( )| A. | 7π | B. | 19π | C. | $\frac{{7\sqrt{7}}}{6}π$ | D. | $\frac{{19\sqrt{19}}}{6}π$ |
分析 通过底面三角形BCD求出底面圆的半径DM,判断球心到底面圆的距离OD,求出球O的半径,即可求解球O的表面积.
解答 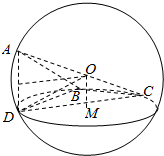 解:△BCD中,BD=1,CD=1,BC=$\sqrt{3}$,所以∠BDC=120°,
解:△BCD中,BD=1,CD=1,BC=$\sqrt{3}$,所以∠BDC=120°,
底面三角形的底面圆半径为:DM=CM=1,
AD是球的弦,DA=$\sqrt{3}$,∴OM=$\frac{\sqrt{3}}{2}$,
∴球的半径OD=$\frac{\sqrt{7}}{2}$.
该球的表面积为:4π×OD2=7π;
故选:A
点评 本题考查球的表面积的求法,球的内接体,考查空间想象能力以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知命题p:0<a<4,命题q:函数y=ax2-ax+1的值恒为正,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8. 为求使不等式1+2+3+…+n<60成立的最大正整数n,设计了如图所示的算法,则图中“ ”处应填入( )
为求使不等式1+2+3+…+n<60成立的最大正整数n,设计了如图所示的算法,则图中“ ”处应填入( )
 为求使不等式1+2+3+…+n<60成立的最大正整数n,设计了如图所示的算法,则图中“ ”处应填入( )
为求使不等式1+2+3+…+n<60成立的最大正整数n,设计了如图所示的算法,则图中“ ”处应填入( )| A. | i+2 | B. | i+1 | C. | i | D. | i-1 |
15.椭圆$\frac{x^2}{m}+\frac{y^2}{4}$=1的焦距为2,则m的值是( )
| A. | 6或2 | B. | 5 | C. | 1或9 | D. | 3或5 |
12.某锥体的三视图如图所示,该棱锥的体积是( )


| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{7\sqrt{3}}{3}$ |
 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC的中点,求AD与平面PAC所成的角的正弦值的大小.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D,E分别在棱PB,PC的中点,求AD与平面PAC所成的角的正弦值的大小. 如图所示,圆O的两弦AB和CD交于点E,作EF∥CB,并且交AD的延长线于点F,FG切圆O于点G.
如图所示,圆O的两弦AB和CD交于点E,作EF∥CB,并且交AD的延长线于点F,FG切圆O于点G.