题目内容
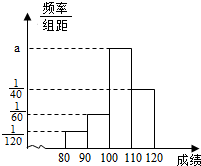 某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,
某校从参加某次数学能力测试的学生中中抽查36名学生,统计了他们的数学成绩(成绩均为整数且满分为120分),成绩的频率直方图如图所示,其中成绩分组间是:[80,90),[90,100),[100,110),[110,120]
(1)在这36名学生中随机抽取3名学生,求同时满足下列条件的概率:(1)有且仅有1名学生成绩不低于110分;(2)成绩在[90,100)内至多1名学生;
(2)在成绩是[80,100)内的学生中随机选取3名学生进行诊断问卷,设成绩在[90,100)内的人数为随机变量X,求X的分布列及数学期望EX.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:应用题,概率与统计
分析:(1)根据频率分布直方图,求出a的值,计算成绩在各分数段内的学生数,计算满足条件的事件的概率即可;
(2)根据题意得出X的可能取值,计算对应的概率,求出X的分布列与数学期望即可.
(2)根据题意得出X的可能取值,计算对应的概率,求出X的分布列与数学期望即可.
解答:
解:(1)由频率分布直方图,得;
10a=1-(
+
+
)×10=
,
解得a=
;
∴成绩在[80,90)分的学生有36×
×10=3人,
成绩在[90,100)分的学生有36×
×10=6人,
成绩在[100,110)分的学生有36×
×10=18人,
成绩在[110,120)分的学生有36×
×10=9人;
记事件A为“抽取3名学生中同时满足条件①②的事件”,
包括事件A1=“抽取3名学生中,1人成绩不低于110分,0人在[90,100)分之间”,
事件A2=“抽取3名学生中,1人成绩不低于110分,1人在[90,100)分之间”,且A1、A2是互斥事件;
∴P(A)=P(A1+A2)=P(A1)+P(A2)=
+
=
+
=
;
(2)随机变量X的可能取值为0,1,2,3;
∴P(X=0)=
=
,
p(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
;
∴X的分布列为
数学期望为EX=0×
+1×
+2×
+3×
=2.
10a=1-(
| 1 |
| 120 |
| 1 |
| 60 |
| 1 |
| 40 |
| 1 |
| 2 |
解得a=
| 1 |
| 20 |
∴成绩在[80,90)分的学生有36×
| 1 |
| 120 |
成绩在[90,100)分的学生有36×
| 1 |
| 60 |
成绩在[100,110)分的学生有36×
| 1 |
| 20 |
成绩在[110,120)分的学生有36×
| 1 |
| 40 |
记事件A为“抽取3名学生中同时满足条件①②的事件”,
包括事件A1=“抽取3名学生中,1人成绩不低于110分,0人在[90,100)分之间”,
事件A2=“抽取3名学生中,1人成绩不低于110分,1人在[90,100)分之间”,且A1、A2是互斥事件;
∴P(A)=P(A1+A2)=P(A1)+P(A2)=
| ||||
|
| ||||||
|
| 9 |
| 34 |
| 27 |
| 170 |
| 36 |
| 85 |
(2)随机变量X的可能取值为0,1,2,3;
∴P(X=0)=
| ||
|
| 1 |
| 84 |
p(X=1)=
| ||||
|
| 3 |
| 14 |
P(X=2)=
| ||||
|
| 15 |
| 28 |
P(X=3)=
| ||
|
| 5 |
| 21 |
∴X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 84 |
| 3 |
| 14 |
| 15 |
| 28 |
| 5 |
| 21 |
点评:本题考查了频率分布直方图的应用问题,也考查了互斥事件的概率以及离散型随机变量的分布列与数学期望的计算问题,是综合性题目.

练习册系列答案
相关题目
已知A,B两地相距150km,某人驾驶汽车以60km/h的速度从A地到达B地,在B地停留1h后再以50km/h的速度返回A地并停在A地,将汽车与A地的距离s(单位:km)表示成时间t(单位:h)的函数为( )
| A、s=60t | |||||||||||
B、s=
| |||||||||||
C、s=
| |||||||||||
| D、s=60t+50 |
已知集合A={x|x>0},B={x|y=log2(1-x2)},则A∩B=( )
| A、(1,+∞) |
| B、(0,+∞) |
| C、(0,1) |
| D、(-1,1) |
已知函数f(x)=2x3-3ax2+8,若f(x)存在唯一的零点x0,且x0<0,则实数a的取值范围是( )
| A、(-∞,0) |
| B、(-∞,0)∪[2,+∞) |
| C、[0,2] |
| D、(-∞,2) |
集合A={x|y=
},B={y|y=log2x,x>0},则A∩B等于( )
| x |
| A、R | B、∅ |
| C、[0,+∞) | D、(0,+∞) |