题目内容
10．下列命题正确的是（ ）| A． | 若直线l上有无数个点不在平面α内，则l∥α | |
| B． | 若直线l与平面α有两个公共点，则直线l在平面内 | |
| C． | 若直线l与平面α相交，则l与平面α内的任意直线都是异面直线 | |
| D． | 平行于同一个平面的两条直线平行 |
分析 根据空间直线与平面的位置关系的定义，分类，及几何特征，逐一分析四个答案的真假，可得答案．
解答 解：若直线l上有无数个点不在平面α内，则l∥α或l与α相交，故A错误；
由公理1可得：若直线l与平面α有两个公共点，则直线l在平面内，故B正确；
若直线l与平面α相交，则l与平面α内的任意直线相交（过交点）或异面（不过交点），故C错误；
平行于同一个平面的两条直线平行、相交或异面，故D错误；
故选：B．
点评 本题以命题的真假判断与应用为载体，考查了空间线面关系，熟练掌握空间线面关系的定义及几何特征，是解答的关键．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
7．
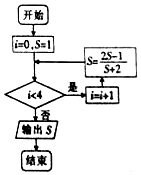执行如图所示的程序框图，输出S的值为（ ）
执行如图所示的程序框图，输出S的值为（ ）| A． | -$\frac{31}{15}$ | B． | -$\frac{7}{5}$ | C． | -$\frac{31}{17}$ | D． | -$\frac{21}{17}$ |
1．
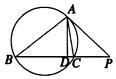如图所示，PA切圆于A，PA=8，直线PCB交圆于C，B，连接AB，AC，且PC=4，AD⊥BC于D，∠ABC=α，∠ACB=β，则$\frac{sinα}{sinβ}$的值等于（ ）
如图所示，PA切圆于A，PA=8，直线PCB交圆于C，B，连接AB，AC，且PC=4，AD⊥BC于D，∠ABC=α，∠ACB=β，则$\frac{sinα}{sinβ}$的值等于（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 4 |
18．某校高三文科学生参加了9月的模拟考试，学校为了了解高三文科学生的数学、外语成绩，抽出100名学生的数学、外语成绩统计，其结果如表：
（1）若数学成绩优秀率为35%，求m，n的值；
（2）在外语成绩为良的学生中，已知m≥12，n≥10，求数学成绩优比良的人数少的概率．
| 外语 | ||||
数学 | 优 | 良 | 及格 | |
| 优 | 8 | m | 9 | |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
（2）在外语成绩为良的学生中，已知m≥12，n≥10，求数学成绩优比良的人数少的概率．
5．下列函数中既不是奇函数也不是偶函数的是（ ）
| A． | y=2x+2-x | B． | y=lg$\frac{1}{x+1}$ | C． | y=2|x| | D． | y=lg（x+$\sqrt{{x}^{2}+1}$） |
某几何体的三视图如图所不，则该几何体的表面积为22π+8．