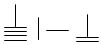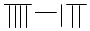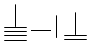题目内容
15.圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-1=0,圆C1与圆C2的公切线有2条.分析 求出两个圆的圆心与半径,判断两个圆的位置关系,然后判断公切线的条数.
解答 解:圆C1的方程即:(x+1)2+(y+4)2=9,圆心C1(-1,-4),半径为3,
圆C2的方程即:(x-2)2+(y-2)2=9,圆心C2(2,2),半径为3,
两圆的圆心距为$\sqrt{9+36}$=3$\sqrt{5}$,正好小于两圆的半径之和,大于半径之差,故两圆相交,
故两圆的公切线只有二条,
故答案为:2.
点评 本题考查两圆的位置关系,两圆相内切的充要条件是:两圆的圆心距等于两圆的半径之差;两圆相内切时,公切线有且只有一条.

练习册系列答案
相关题目
3.函数$y=\frac{{|{x+1}|-|{x-1}|}}{{\sqrt{x^2}+1}}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
10.下列命题正确的是( )
| A. | 若直线l上有无数个点不在平面α内,则l∥α | |
| B. | 若直线l与平面α有两个公共点,则直线l在平面内 | |
| C. | 若直线l与平面α相交,则l与平面α内的任意直线都是异面直线 | |
| D. | 平行于同一个平面的两条直线平行 |
4.设向量$\overrightarrow{a}$=(2,0),$\overrightarrow{b}$=(1,1),则下列结论中正确的是( )
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$ | C. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ |
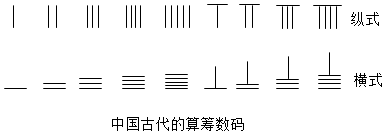
 ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )